2020-12-26

【神童】サヴァント・アレニウスの生誕

科学者の物語

本日も、りけいのりがお届けします。

今回は、(一部の理系にとっては言わずと知れた)大物理化学者、サヴァント・アレニウスに関するお話です。

アレニウスといえば、

アレニウスの式：化学反応の速度と温度の関係式
アレニウス効果：α毒素の残存に関する効果

など、様々なところに名前を残している、スウェーデンの物理化学者です。実は、温室効果ガスと地球温暖化という概念も、彼が最初に提唱しています。

彼は、一体どのような人生を歩んだのでしょうか。

f:id:ReK2Science:20201022161956p:plain

【神童】サヴァント・アレニウスの誕生
その人生
おわりに
- 参考文献

【神童】サヴァント・アレニウスの誕生

まずは、アレニウスの略歴です。

f:id:ReK2Science:20200927142719p:plain — サヴァント・アレニウス

国籍はスウェーデンで、専門は化学および物理学としています。1903年に、ノーベル化学賞も受賞しています1)。

彼の人生は、スウェーデンのウプサラ近郊、Vikという町で生まれます。

f:id:ReK2Science:20201023090155p:plain — アレニウスの故郷vik

湖に面した、非常に小さな町であることが分かります。

ウプサラ大学の測量技師を務める父親の息子として誕生しました。中でも、次のような振動エピソードがあります、

3歳：独学で文字を読めるように。父親をまねて、算術ができるように。

学校に入学するやいなや、5年生に飛び級。物理学や数学で優れた才能を発揮。

(世界の偉人館、アレニウス2))

恐ろしきアレニウス。3歳までに、どの様な教育を受けていたのか非常に気になります。

その後の略歴は次の通りです。

名門、ウプラサ聖堂学校に入学

1878年、学位取得：ウプサラ大学

1884年、博士号取得：ウプサラ大学

1884年、ウプサラ大学にて名誉取得

1886年、スウェーデン王立科学協会から旅費手当を受給し、様々な研究室に滞在 (ポスドク)

ウィルヘルム・オストワルトの研究室 (ラトビアのリガ大学、ドイツのライプツィヒ大学)

フロイントリッヒ・コールラウシュの研究室 (ドイツのユリウス・マクシミリアン大学ヴュルツブルク)

ルートヴィッヒ・ボルツマンの研究室 (オーストリアのグラーツ大学)

ヤコブ・ヘンリクス・ファントホッフの研究室 (オランダ、アムステルダム大学)

(Elisabeth Crawford (2020), 1))

以上から、理系大学生であれば必ずや耳にしたことのある大科学者の基で、科学者としてのキャリアを積んでいったことが分かります。非常にうらやましいですね。

その後、彼は次の機関に所属しました1)。

スウェーデン王立科学研究所、物理学研究所
ストックホルム大学：宇宙物理学 (約5年間)
State Serum Institute (コペンハーゲン)：免疫化学の研究

重要なのは、アレニウスが物理化学という学問の立役者であるということです。彼は、溶液中での電解質の挙動について、電離説を提唱しました。

電離説: 電解質は電場をかけなくても水中でイオンに解離しているとする説 (ブルーバックス編集部3))

電離というこの現象は、静電気的な考察 (物理学) と化学的な考察に基づくことから、物理化学という学問領域の範疇となります。

この他にも、"アレニウスの式"を提唱したとして、彼の名前は今後も語り継がれていくことでしょう。しかし、この"アレニウスの式"の根幹概念は、既にファントホッフが提唱していたとされています4)。つまり、化学反応の温度依存性に関する式は、ファントホッフの式と呼ばれていたかもしれません。しかし、浸透圧に関するファントホッフの式、化学平衡定数に関するファントホッフの式と、ファントホッフは既に多くの業績を挙げています。

アレニウスの式を提唱していた論文が投稿された学会誌がオストワルトの傘下にあり、アレニウスの師としてファントホッフがいたことを鑑みると、色々な人間関係が見えてきます。

りけいのりとしては、アレニウスが先生方に可愛がられていたのではないか、と考えております。

その人生

最前線に立つ科学者として、分野にとらわれることなく活躍したアレニウス。彼の科学に対するアグレッシブさは、電気化学に限りません。

例えば、彼は初めて、二酸化炭素のような温室効果ガスと地球温暖化の関係について予想をしていました5)。地球温暖化とは、太陽光線の内の赤外光が温室効果ガスの分子振動を促進することで発生する、地球表面の気温上昇現象です。地球という宇宙に浮かぶ惑星を温室ととらえた、少しオシャレな表現です。

勿論、そのモデルには大きな修正が必要となったのですが、100年前から地球温暖化について予言していたことに、大きな価値があります。

また、微生物学においても大きな貢献をしています。アレニウスは、アレニウス効果という現象を発見しています。

耐熱性とは、耐熱性溶血毒 (Thermostable Direct Hemolysin)に代表される、加熱に対して失活しないような性質。

60℃の加熱により毒素は失活し、さらに高温で加熱処理を行った後に毒素活性が残存するという、耐熱性に関する現象。→アレニウス効果

(Spring8, 6))

アレニウス効果は、現在、タンパク質のフォールド・アンフォールドの観点から、原子レベルで明らかになっています5)。

おわりに

非常に幅広い分野で功績を挙げたサヴァント・アレニウス。彼の科学に与えた影響は計り知れません。

しかし、ここで真に特筆すべきは、彼の飽くなき知的好奇心ではないでしょうか。物理学、化学、微生物学と、彼は学問の枠にとらわれず、多くの問題に取り組みました。揺るぎないその探求心は、地球温暖化という未来を見通すに至っています。

今回の記事では、サヴァント・アレニウスの人生と業績についてお伝えしました。

アレニウスの名を冠した、アレニウスの式については以下の記事にて解説しているので、参考にしてみて下さい。

www.rek2u.com

以上、りけいのりがお届けしました。

参考文献

1)Elisabeth Crawford (2020), Svante Arrhenius, Swedish chemist, Britannica, Accessed: 2020/10/23.

www.britannica.com

2) 世界の偉人館、アレニウス、Accessed: 2020/10/23.

greatman.merrymall.net

3) ブルーバックス編集部 (2020)、2月19日　スウェーデンの化学者アレニウス誕生（1859年）、Accessed: 2020/10/23.

gendai.ismedia.jp

4) 小岩昌宏 (2000), アレニウスと反応速度論 -伝記に見るその人物像-, まてりあ, 39, 1.

https://www.jstage.jst.go.jp/article/materia1994/39/1/39_1_58/_pdf

5) 合同会社ワライト (2018), 地球温暖化を最初に訴えた科学者はアレニウス, Accessed: 2020/10/23.

www.walight.jp

6) Spring8 (2010), 食中毒原因菌の腸炎ビブリオの毒性は加熱してもなぜ消えないのか？－腸炎ビブリオの耐熱性溶血毒（TDH）の構造解明－（トピック）、Spring 8、Accessed: 2020/10/23.

www.spring8.or.jp

2020-12-25

【オリバー・ヘヴィサイド】無頼の物理学者

科学者の物語

本日も、りけいのりがお届けします。

皆さんの夢は何でしょうか？

有名人になる、お金持ちになるというような小学生じみたものから。

サラリーマンになりたい公務員になりたいと言った堅実的なもの。

海賊王になるや宇宙人になると言った頭のおかしいもの。

様々でしょう。

私の夢は、晴れた日には畑を耕し、雨の日には本を読む、晴耕雨読を地で行くような生活をするというものです。

さて、彼が晴れた日に農業をしていたかはわかりませんが、その一生の殆どを自宅における研究に捧げた、変態的な物理学者がここにいます。

その名は、オリヴァー・ヘヴィサイド。何者にも頼らない無法者という意味で、無頼の物理学者と、ここでは呼びましょう。

理系の人なら、一度はその名を聞いたことが有るはず。その業績のいくつかを箇条書するとこんな感じです。

ヘヴィサイドの階段関数
ヘヴィサイドの展開定理（ヘビサイドの展開定理 | 高校数学の美しい物語）
線形微分方程式における演算子法
ポインティング・ベクトル（電磁場のエネルギーの流れ密度）の独立な発見
マクスウェル方程式をベクトル解析に翻訳することへの貢献（ヘヴィサイドとギブズによる仕事と言われる。）

みなさんも心当たりの有るものがいくつか有るのではないかと思います。特に今では物理数学と呼ばれている分野において、多くの功績を残したことがわかります。

この記事では、彼の業績の解説をするのではなく、彼の半生を詳しく見ていきたいと思います。

目次は以下のようになっています。

オリヴァー・ヘヴィサイドという人
まとめ
参考文献

それでは早速、無頼の物理学者ヘヴィサイドの半生を見ていきましょう！

オリヴァー・ヘヴィサイドという人

f:id:ReK2Science:20201017165411j:plain — SuperGirl at en.wikipedia, Public domain, via Wikimedia Commons

オリヴァー・ヘヴィサイド（1850〜1925）

聴覚障害を負った幼少期

オリヴァー・ヘヴィサイドは、ロンドンにおいて、木工彫刻師・水彩画家である父トーマス・ヘヴィサイドと、近所の子供向けの私塾を開いた母レイチェルエリザベスの間に、4人兄弟の末っ子として生まれました。幼少期に、猩紅熱（小児に多く見られる発疹を伴う伝染病）に見舞われ、一時的に耳が聞こえなくなります。このせいで、彼は他の子どもたちと上手く交わることができず、不遇の幼年時代を過ごすことになります。

学校を辞めざるを得なくなる

彼の育った地域は、作家チャールズ・ディッケンズも幼年時代に不遇を強いられた、ロンドンにあってもとても貧しい地域であり、両親はオリヴァーを学校に通わせるのも大変でした。祖父母の遺産が入ったことで、別の場所に引っ越し、少しは暮し向きもよくなったようです。

オリバーは、優秀で学校でも500人中5番目になるほどだったようですが、両親はオリバーを学校に通わせるほどのお金が捻出できなくなり、16歳にして、教育課程からドロップアウトします。

叔父ホイートストンとの出会い

f:id:ReK2Science:20201017195106j:plain — Samuel Laurence, Public domain, via Wikimedia Commons

チャールズ・ホイートストン（1802〜1875）

恵まれない時代が続いた彼は、他方で特権的地位を持っていたともいえます。それは、叔父に、ロンドンのキングスカレッジの物理学者であり、電気通信の発明家でもあった、チャールズ・ホイートストンがいたからです。

ホイートストンブリッジと聞けば、理系の多くの人は聞いたことが有ると思います。キルヒホッフの法則の威力が発揮される、もはや大学入試では典型的な問題である、あのホイートストンブリッジです。

ヘヴィサイド家の息子たちは、皆ホイートストンに頼り切りだったのですが、オリヴァーもご多分にもれず、既にホイートストンの事業を手伝っていた兄の手伝いを始め、1868年にはデンマークの大北電信会社（現在は改称してGN）に就職します。

何故か仕事をやめる

f:id:ReK2Science:20201017192517p:plain

当時電気通信の分野は活発で、大北電信会社には、高度な設備が整っていました。そこでの仕事において、オリヴァーは自然と電気測定や電気通信の分野に興味を持ち始めたのです。

しかし、1874年当時24歳で、彼は突然仕事を辞めてしまいます。会社では能力の有るエンジニアだったようですが、自分の能力に見合わない仕事は断るなど偏屈な面もあり、また体調も芳しくないことがおおかったようです。それが理由だったのか、仕事を辞め、その後は、実家に戻って空き部屋にこもりきります。

しかし、そこで何もしないわけではなく、仕事をする内に興味を持ち始めた、電気学の分野の研究を日夜続けたのです。もしかしたら、研究に没頭したいがために仕事を辞めたのかも知れません。本人に聞いてみないことにはわかりませんが。

悠々自適の年金生活から、奇行の目立った晩年へ

兄の援助を受けながら自宅での研究生活を続けたオリヴァーは、その革新的な仕事から次第に認知を得て、現在にも残る偉大な業績をあげていきます。1891年には英国王立協会フェローに任命され、1896年には科学者仲間の尽力で、年に120ポンド（後に220ポンド）の年金を受け取るまでになります（1894年には一度受け取ることを拒否している）。

しかし、後年になると体調の悪化や、多少の妄想の症状が現れ、物理学者として仕事は、実質的に1905年には止まっていたようです。

晩年は一人で、貧しいにもかかわらず大きな家に住み、庭や部屋は散らかりっぱなし。料理もしないので、親しい近所の警官が料理を運びに来ていたという話もあります。手紙に'W.O.R.M'というへんてこな名前を書いたり、爪をピンクに塗るなど、の奇行も目立っていたようです。

まとめ

無頼の物理学者は、孤独を愛し偏屈であったが故に、学問的常識などというものに忖度すること無く、当時としては革新的な業績をいくつも挙げられたのだと思います。失意の晩年はある意味で必然だったのかも知れません。天才と変人は紙一重の違いといいますが、本質的には一緒なのでしょう。本質的な変人だったオリヴァー・ヘヴィサイドは、そうだからこそ天才たり得て輝かしい中年時代を過ごし、盛者必衰の理には逆らえずに、晩年ただの変人と化した。むしろ尊敬を込めて、私は、彼の人生が羨ましいと思っています。

参考文献

「Oliver HeavisideA first-rateoddity」 Bruce Hunt, University of Texas

http://fep.if.usp.br/~fbrandt/fisica4/OliverHeavside.pdf

WikipediaのOliver Heavisideの記事

Oliver Heaviside - Wikipedia

MacTutor History of Mathematics Archive(約3000人に及ぶ数学者の経歴が載っているページ)

https://mathshistory.st-andrews.ac.uk/Biographies/Heaviside/

2020-12-24

【アリストテレス】と【カイメン】

科学者の物語

本日も、りけいのりがお届けします。

アリストテレス。

誰もが一度は耳にしたことがある哲学者でしょう。多くの人は、教科書で見たあの彫刻の人。くらいのイメージしか無いかも知れません。

今回の記事では、まず最初に、アリストテレスという人がどのような人物であったかを説明します。

その次に、え？そんなことまでやってたの？と驚くこと必至な、彼による「動物誌」という著作に触れます。哲学的文脈で語られることの多いアリストテレスですが、「動物誌」を訳した島崎三郎はその序文でこう言っています。

アリストテレースの動物学書は，彼の学問的立場が本質的には生物学を基礎としていることから見て，自然科学のみならず哲学的論文の理解のためにも重要なものであり，西洋の科学文明の礎石とも言うべき書である.

つまり、彼の哲学的態度が、生物学を元にしていると言っています。これは、中々驚くべきことなのではないでしょうか。

目次は以下のようになっています。

アリストテレスという人
- プラトンの弟子として
- アレクサンドロス大王の家庭教師として
アリストテレス生物学とカイメン
まとめ
参考文献

それでは、まず、アリストテレスという人物がどのような人かを説明していきます！

アリストテレスという人

f:id:ReK2Science:20201017141028j:plain — After Lysippos, Public domain, via Wikimedia Commons

アリストテレス（384BC〜322BC）

西洋最大の哲学者と言われ、同時に「万学の祖」とも言われます。

彼の研究をした学問は、倫理学・政治学、論理学・形而上学、宇宙論・天文学、生物学、果ては詩学・演劇学などに及びます。

過去に遡ると、知の巨人たちは今では考えられないほど様々な学問に渡って、研究を行っていたりしますが（ニュートンは数学者であり物理学者であり天文学者であり神学者でもあった）、彼の研究領域の広範さは他に類を見ないでしょう。

この広範な学問への興味は、人間の本性が「知を愛する」（フィロ・ソフィア）にあると考えた彼をよく象徴しているといえます。

プラトンの弟子として

アリストテレスは、マケドニアの王に仕える医者であった父と、裕福な家庭の出身であった母の下に生まれました。後に生物学に深い興味を持ち、精緻な動物分類をおこなったのも、父から医学や生物に関して様々な知識を受け取っていたからかも知れません。

そんな彼は、17(18とも）歳の時に、プラトンが主催していた学校「アカデメイア」の門を叩いて、そこの学生となります。彼らの関係はおおよそ20年つ続いたと言われ、師から学んだ「学校の精神」を受け継いだアリストテレスは、のちにリュケイオンという学校を作ります。アリストテレスの著作は、公衆へ向けたものと、講義用のものとに分けられます。実は現在残っている彼の著作の多くが、リュケイオンにおける講義を目的としたものなのです。

教科書では、よく師のプラトンのイデア論を批判したと取り上げられます。これは、師の論を全く拒否したというより、それを基盤として彼独自の哲学を作り上げる糧となったということでしょう。

アレクサンドロス大王の家庭教師として

当時、マケドニアの王であったフィリッポス2世は、息子であるアレクサンドロスの家庭教師として、アリストテレスを指名します。この学問における師弟関係は、7年間も続いたと言われます。

アレクサンドロスは、アリストテレスから「フィロ・ソフィア」の精神を受け継いだのかも知れません。後に、父フィリッポス2世の意志を受け継ぎ、幾多の政治的困難を経て、大帝国を作り上げました。彼は、非常な読書家となり、戦地に赴くときも本を持ち歩いたと言われています。また、各地で植物や動物を見つけるとアリストテレスの元へ送ったりと、その関係は終生続きました。

アリストテレス生物学とカイメン

動物誌 (上) (岩波文庫)

作者:アリストテレース
発売日: 1998/12/16
メディア: 文庫

動物誌 (下) (岩波文庫)

作者:アリストテレース
発売日: 1999/02/16
メディア: 文庫

アリストテレスは「動物誌」と呼ばれる著作を残しています。この動物分類は、古代世界のどこを見渡しても（古代中国や古代インドをみても）無いほど詳細に書かれた、当時としては唯一無二の業績と考えられています。

この著作の中では、約120種の魚や60種の昆虫を含む、500以上の動物に関する知見が、詳らかな観察によって記述されています。

f:id:ReK2Science:20201017145151j:plain — カイメン

例えば彼は、動物的な特徴の乏しい'動物'として、「カイメン」を挙げています。イソギンチャクやホヤなどと同じ固着性動物と呼ばれる分類にあり、動きに乏しくまた体内の構造も非常に単純な生物です。

細長い形状をしていて、群衆している姿はドレッドヘアーのようです。海の底に張り付いており、外見上は全く動くことがなく、ただ波に揺られるだけです。体の各部分に開いた穴から、細胞表面に有る鞭毛の働きによって、体内に水流を作り出します。そうしてできた水流から、水中に含まれる栄養素を吸収しており、できるだけ動かない引きこもりニートの元祖とも言えるかも知れません。

実際に現在では、襟鞭毛虫（動物とはいえない）と呼ばれる生物が集まってできたような構造をしていることや、遺伝子的な解析から、カイメンは「動物」の最も原初の一つだと考えられています。

アリストテレスは、その細緻な観察によって、植物とも見間違えかねないカイメンを、現代的な見方と同じ「動物」に分類したことになります。彼の徹底的な観察の姿勢は、島崎がいうように科学文明の礎石たりうるに十分だったと言えるでしょう。

まとめ

以上アリストテレスという人がどんな人であったか、そして彼の業績の一つ動物の観察について書いてきました。アリストテレスが動物観察を詳しくしてそれに関する大部の著作まで残しているというのは、中々の驚きなのではないでしょうか。筆者も実際その事実に驚いて、この記事を書いた次第です。アリストテレスという人に漠然としたイメージしか持っていなかった人が、なんとなくどのような人物だったかを知ることができたなら幸いです。

参考文献

・「アリストテレス生物学における動物と植物の連続性について」　中村　公博

http://file:///tmp/mozilla_kouta0/AN10065043-20050000-0001.pdf

・Stanford Encyclopedia of PhilosophyのAristotleというページ

Stanford Encyclopedia of Philosophy

・Ancient History EncyclopediaのAristotleというページ

Ancient History Encyclopedia

・日本語・英語版wikipediaのアリストテレスのページ

・アリストテレス　「動物誌」　島崎三郎訳　岩波文庫

・放送大学テキスト「動物の科学」　二河成男・東正剛著著

2020-12-23

【科学者列伝】Introduction

科学者の物語

本日も、りけいのりからお届けします。

新カテゴリー開設のお知らせです。

質問
人物を知ることのすすめ
最後に

質問

ここで唐突な質問。

皆さんは人間ですか？………………

……は？当たり前だろと、どこからか聞こえる気がします。

不思議と、

実は……火星人でして……先日はうちのUFOがお騒がせしてすいません…という声や、

実は……妖怪でして……なんでもかんでもぼくらのせいにされて困っていて、早く人間になりたいです…という声や、

実は……虚数でして……存在するのか否かとかいう論争に巻き込まれていて、早く実数になりたいです…という声が、

控えめながらする気もします。

ちなみに驚くなかれ！　　　

私は人間です。

さて唐突な質問に、この記事は一体何の記事だったかわからなくなってしまった人もいるかも知れません。

一応新カテゴリー開設記事でした。

しかし、そのテーマ内容に関連して、今一度皆さんがやっぱり人間であることを確認しておきたかったのです。

さて、その人間に関連したカテゴリー、その名は、

開設を告げるスライド写真

科学者列伝です。

私は、ずっと思っていました。科学者がおもろい！と。科学における大発見や、偉大な理論の創出には、いつだって人間が関わっているのです。その歴史をたどってみると、そこには人間ドラマや、ただの人間が有るのです。

そして、そういった科学者は大概、並ではない、とんでもない人物たちです。幼少期に自力で文字が読めるようになったものもいれば、小学校の先生が出した難問を一瞬で解いたものもいたり。はたまた、話しかけても全く話さないものもいたり、ずっと実家に引きこもって研究し偉大な業績をあげたものもいる。夢の中で神に数式を教えてもらうものや、無限を覗き無限に覗かれ精神を病んだものもいた。

しばしば、科学者の半生が小説や映画になるのも、彼らの発見が偉大なだけでなく、一人の主人公として描くに足るだけの、突出した特徴や性格を持っているからです。

例えば、アラン・チューリングを主人公にした『イミテーション・ゲーム/エニグマと天才数学者の秘密』（2014）、シュリニヴァーサ・ラマヌジャンを主人公にした『奇蹟がくれた数式』（2016）などは、良い例です。

イミテーション・ゲーム／エニグマと天才数学者の秘密(吹替版)

発売日: 2015/10/02
メディア: Prime Video

奇蹟がくれた数式(字幕版)

発売日: 2017/03/24
メディア: Prime Video

人物を知ることのすすめ

皆さんは、歴史的書物の記述方式に、「編年体」と「紀伝体」というものが有るのを知ご存知でしょうか？

「編年体」は、その名からも察せるとおり、起こった出来事を、時間軸に沿って順番に記述していく方式です。

対して「紀伝体」は、その名前からは、どのようなものかを察することは難しいと思います。簡単にいうと、一つの国や個々の人物ごとに、起きた出来事を記していく記述方式です。本来は特に中国や日本で用いられた歴史書の形式で、その中身が、一国の王や皇帝を中心として起きた出来事を記述した「本紀」、国に仕えた官僚や武将を中心として起きた出来事を記述する「列伝」、にわけられます。この後ろの漢字を取って、「紀伝体」と名付けられました。

長い中国の歴史では、人物を中心としたこの「紀伝体」が、司馬遷の『史記』以降、国家の歴史書の形式として、中心を担ってきました。

つまり、編年体という形式がありながらも、紀伝体という、人間中心の記述方式が、古来から愛されていたわけです。

私は、ここに必然性が有ると思います。無機的に整理された情報は、確かに、正確にすばやく情報をインプットしたいときには優れています。しかし、人間の脳みそはそれほど賢くできていない。学習の過程で出てきた人物に強く共感しながら学んだり、脱線した無駄な情報と共に学んだりしたほうが、しばしば、記憶の中にいつまでも残っているということが有ると思います。

科学全般に関して勉強をしているときも、よく定理や方程式に名前が出てくるあの人だったり、なんかよく名前も聞いて有名なのも知っているけど、未だに勉強していて出てきたことがないあの人。そんな人たちの面白い半生や性格・特徴を知ることで、今までやっていたつまらない勉強に、鮮やかな色が付いて、学問がより楽しくなってきます。学んだこともより記憶に残って、学習効率も上がるでしょう。

だから皆さんに、人を中心にして、科学を捉えてみるということを、是非してほしいのです！

最後に

この新カテゴリー「科学者列伝」、確実に理系の人でも文系の人でも楽しんでいただけると思います。

また、その人が行った科学的業績の専門的な説明というよりも、その人物自体のことを取り上げて、その人がどのような人生を送ってきたのか。どんな人だったのか。ということを中心とした記事を書いていこうと思っております。ですので、背景知識がなくても楽しめる内容となっています。

ぜひ、「科学者列伝」を通して、科学者の人間としてのあり方を楽しんでいただけると、嬉しいです。

科学の歴史はある意味では錯覚と失策の歴史である。偉大なる迂愚者（うぐしゃ）の頭の悪い能率の悪い仕事の歴史である。

頭のいい人は批評家に適するが行為の人にはなりにくい。すべての行為には危険が伴なうからである。けがを恐れる人は大工にはなれない。失敗をこわがる人は科学者にはなれない。

科学もやはり頭の悪い命知らずの死骸（しがい）の山の上に築かれた殿堂であり、血の川のほとりに咲いた花園である。（寺田寅彦　『科学者とあたま』）

寺田寅彦科学者とあたま (STANDARD BOOKS)

作者:寺田寅彦
発売日: 2015/12/14
メディア: 単行本

2020-12-22

【プログラミング】ニュートン法をC言語で実行してみよう！【数値解析：ニュートン法②】

プログラミング

本日も、りけいのりからお届けします。

今回も，

解けない方程式を解く！

をテーマにしていきます．

まず，ニュートン法の復習です！

その方程式を以下のように変形します．

未知数を $\displaystyle{ x }$ とした，方程式を以下のように変形します．

$\displaystyle{ f(x) = 0}$

次に初期値 $\displaystyle{ x^{(0)} }$ を定め，以下の式で繰り返していきます．

$\displaystyle{ f(x) = 0}$

$\displaystyle{ x^{(k+1)} = x^{(k)} - \frac{f(x^{(k)})}{f'(x^{(k)})} }$

以上です．

ここで，このニュートン法には繰り返しの処理が必ず必要です．場合によっては50回，100回繰り返す必要が出てきます．このため，コンピュータを使っていきます！

今回は，ニュートン法での方程式の解法を，C言語でコンピュータでの計算を詳しく行っていきます．

C言語のプログラムの実行などのついては，過去記事を参照してください！

f:id:ReK2Science:20200919023135j:plain

問題設定
ニュートン法
計算例
おわりに
- 参考文献

問題設定

それでは，さっそくやっていきましょう．

ソースコード

#include<stdio.h>
#include<math.h>
#pragma warning(diaable:4996)
#define PI 3.141592

int main(void)
{

 double a = 26600;
 double e = 0.75;
 double u = 398600.5;
 double t0 = 0;
 double t[25];
 double M0 = 0;
 double M[25];
 double E[25];
 double n = 0;

 int i, j= 0;

 n = sqrt(u / pow(a, 3));
 printf("%lf\n", n);

 for (i = 0; i <= 24; i++)
 {
 t[i] = 1800 * i; M[i] = n * (t[i] - t0) + M0;
 E[i] = 0;
 for (j = 0; j < 50; j++)
 E[i] = E[i] - (E[i] - e * sin(E[i]) - M[i]) / (1 - e * cos(E[i]));
 }

 //for (i = 0; i <= 24; i++)
 // printf("t-t0 = %lf\n   M = %lf\n   E = %lf\n", t[i]/60, M[i]*(180/PI), E[i]*(180/PI));

 for (i = 0; i <= 24; i++) printf("%lf\n", M[i] * (180 / PI));
 for (i = 0; i <= 24; i++) printf("%lf\n", E[i] * (180 / PI));

 return 0;
}

\\\

皆さん，以下の式を解いてみましょう！

[tex:\displaystyle{ 8x + 4 = 36 }]

中学校一年生の一次方程式の問題ですね．答えは次のようになりますね．

[tex:\displaystyle{ x = 4 }]

これは，線形方程式(linear equation)に分類されます．これに対して，非線形方程式(nonlinear equation)もあります．この，線形と非線形の言葉については別の機会に説明しますが，簡単に紹介すると，厳密には違いますが，なんとなく線形は「直線的」というイメージでいいと思います．話を戻します．非線形方程式の例は以下の通りです．

[tex:\displaystyle{ x^4 - 7x^3 + 4x^2 - x + 5 = 0}]

[tex:\displaystyle{ \frac{ 4x - 5 }{ x^2 - 5x +5 } + \frac{ x + 2 }{ x^2 - 1} + 3x = 0}]

[tex:\displaystyle{ ( x - 3 )^{\frac{5}{2}} + ( x^2 - 5 )^{\frac{4}{3} }= 0 ) }]

[tex:\displaystyle{ e^x - sin x - 2 = 0}]

もちろん，非線形方程式のすべてが解くことができないわけではありません．解くことができる方程式もたくさんあります．しかし，これから，紹介する方法を使えば，だいたいの方程式を解くーその方程式を満たす未知数の値を導くーことができます．もちろん，場合によっては解けない場合がありますが，普通は解けます．

ニュートン法

それでは，解けない方程式を解いていく手順を紹介します．まず，今回はニュートン法の手順を説明しますが，ほかにも，反復法と呼ばれる手順もあります．

まず，未知数を[tex:\displaystyle{ x }]として，その方程式の項を左辺にまとめ，右辺をゼロにしたものを

[tex:\displaystyle{ f(x) = 0}]

と表現します．この方程式を満たす，[tex:\displaystyle{ x }]を近似的に求めていきます．

ここで，このニュートン法の理解のコツとして，図を用いて説明していきます．この[tex:\displaystyle{ f(x) }]を関数として，

[tex:\displaystyle{ y = f(x) }]

と考えると，求める解は以下の図の[tex:\displaystyle{ y = f(x) = 0}]を満たす点，つまり，軸との交点ということがわかります．

では，具体的な手順を見ていきます．

ソースコード

#include <stdio.h>
#pragma warning(disable:4996)

int main(void)
{
printf("hello world\n");
return 0;
}

初期値[tex:\displaystyle{ x^{(0)} }]の点で垂線を引きます．この[tex:\displaystyle{ x^{(k)} }]は，微分や累乗を表しているのでなく，ｋ回目の計算で求めた解という意味で，第ｋ次近似解とか言われます．この初期値[tex:\displaystyle{ x^{(0)} }]は，適当に決めます．大体の場合は，どんな値にしても最終的にはうまくいきます．
曲線[tex:\displaystyle{ f(x) }]との交点をAとします．
A点での接線の方程式を立てます．
[tex:\displaystyle{ y - f(x^{(0)} )= f'(x^{(0)}) ( x - x^{(0)}) }]

より

[tex:\displaystyle{ y = f'(x^{(0)}) ( x - x^{(0)}) + f(x^{(0)} ) }]
その接線と水平軸との交点をBとし，座標値[tex:\displaystyle{ x^{(1)} }]とおきます

上の接線の式より次のように求まります．

[tex:\displaystyle{ 0 = f'(x^{(0)}) ( x - x^{(0)}) + f(x^{(0)} ) }]
線の方程式を立てます．
[tex:\displaystyle{ x^{(1)} = x^{(0)} - \frac{f(x^{(0)})}{f'(x^{(0)})} }]
この操作を繰り返す．
一般に，[tex:\displaystyle{ x^{(k+1)} }]は次のように表せます．
[tex:\displaystyle{ x^{(k+1)} = x^{(k)} - \frac{f(x^{(k)})}{f'(x^{(k)})} }]
操作を繰り返すにつれて，[tex:\displaystyle{ x^{(k+1)} }]は限りなく[tex:\displaystyle{ f(x) = 0}]の解に近づいていきます．

以上です！こんな手順です！

計算例

手順はわかったけど，まだなんかしっくりこないなあ，，，って人が多いと思います．

それは当然で，実際にこれを利用した具体例がないとイメージがわかないと思います．

今回は，次の具体例を，計算してみましょう．

[tex:\displaystyle{ x^{2} = 3 }]をニュートン法で解け．

この問題は，別に数値解析でなくても解けますね．この解は，

[tex:\displaystyle{ x = \pm{\sqrt{3}} }]

ですね！だいたい，1.7320508・・・（ひとなみにおごれや）ですね．

では，これを，ニュートン法を用いて解いたとき，どうなるか見ていきましょう．

まず，次のように変形します．

[tex:\displaystyle{ f(x) = x^{2} - 3 = 0 }]

この時，以下のように計算できます．

[tex:\displaystyle{ f'(x) = 2 x }]

これらを用いて，以下のようにニュートン法の計算を行います．

[tex:\displaystyle{ x^{(k+1)} = x^{(k)} - \frac{ (x^{(k)})^{2} - 3 }{ 2 x^{(k)} } }]

となります．ちなみにですが，私の場合以下のように変形します．計算ミスを減らすためです．累乗の計算をしなくて済みます．

[tex:\displaystyle{ x^{(k+1)} = \frac{ 1 }{ 2 } ( x^{(k)} + \frac{ 3 }{ x^{(k)} } ) }]

では，さっそく計算してみましょう．ここでは，初期値を[tex:\displaystyle{ x^{(0)} = 2.0 }]とします．

\begin{eqnarray} x^{(1)} &=& \frac{ 1 }{ 2 } ( x^{(0)} + \frac{ 3 }{ x^{(0)} } ) \\ &=& \frac{ 1 }{ 2 } ( 2 + \frac{ 3 }{ 2 } ) \\ &=& 1.75 \end{eqnarray}

次も行きます！

\begin{eqnarray} x^{(2)} &=& \frac{ 1 }{ 2 } ( x^{(1)} + \frac{ 3 }{ x^{(1)} } ) \\ &=& \frac{ 1 }{ 2 } ( 1.75 + \frac{ 3 }{ 1.75 } ) \\ &=& 1.732142857 \end{eqnarray}

\begin{eqnarray} x^{(3)} &=& \frac{ 1 }{ 2 } ( x^{(2)} + \frac{ 3 }{ x^{(2)} } ) \\ &=& \frac{ 1 }{ 2 } ( 1.732142857 + \frac{ 3 }{ 1.732142857 } ) \\ &=& 1.73205081\end{eqnarray}

以上です！だいぶ，[tex:\displaystyle{ \sqrt{3} }]に近い値が計算で求まってきましたね！これをずっと繰り返すと，さらに精度が高まってきます！

ですが，ここで，気づいてほしい問題が2つあります．

1つ目は，もう一つの解の[tex:\displaystyle{ - \sqrt{3} }]の結果が得られなかったこと.ちなみに今回も含め，大体の場合，初期値の与え方で，ほかの解も得られます．

2つ目は，初期値を[tex:\displaystyle{ x^{(0)} = 0.0 }]とすると，分母がゼロとなり，計算ができないこと．

今回はそこまで詳しい考察はしませんが，ニュートン法を利用される際は，正解が複数個あるときの初期値の与え方や，初期値の与え方による計算の変化，について検討が必要です．

おわりに

いかがでしたか?

もし，どうしても解けない方程式があなたの目の前に現れても，あっても今日の方法を使えば，何とか太刀打ちできます．

しかし，このニュートン法には繰り返しの処理が必ず必要です．今回の計算例では，すぐに大体の値に答えが収束しましたが，場合によっては50回，100回繰り返す必要が出てきます．このため，コンピュータを使っていきます！

次回は，ニュートン法での方程式の解法を，本格的にC言語でコンピュータでの計算を詳しく行っていきましょう！

www.rek2u.com

本日も、りけいのりがお届けしました。

参考文献

1)高橋麻奈『やさしいC　第4版』　風工舎

www.amazon.co.jp

2)安田仁彦『数値解析基礎』　コロナ社

www.amazon.co.jp

2020-12-21

【プログラミング】解けない方程式を解きたい！【数値解析：ニュートン法①】

プログラミング

本日も、りけいのりからお届けします。

今回は，

解けない方程式を解く！

をテーマにしていきます．まずは，解けない方程式ってどんなものかを説明し，具体的に解く手順を説明していきます．

そして，次回以降，実際にC言語でプログラムを書き，解いていきます．

f:id:ReK2Science:20201001230316p:plain

解けない方程式
ニュートン法
計算例
おわりに
- 参考文献

解けない方程式

皆さん，以下の式を解いてみましょう！

$\displaystyle{ 8x + 4 = 36 }$

中学校一年生の一次方程式の問題ですね．答えは次のようになりますね．

$\displaystyle{ x = 4 }$

$\displaystyle{ x^4 - 7x^3 + 4x^2 - x + 5 = 0}$

$\displaystyle{ \frac{ 4x - 5 }{ x^2 - 5x +5 } + \frac{ x + 2 }{ x^2 - 1} + 3x = 0}$

$\displaystyle{ ( x - 3 )^{\frac{5}{2}} + ( x^2 - 5 )^{\frac{4}{3} }= 0 ) }$

$\displaystyle{ e^x - sin x - 2 = 0}$

ニュートン法

まず，未知数を $\displaystyle{ x }$ として，その方程式の項を左辺にまとめ，右辺をゼロにしたものを

$\displaystyle{ f(x) = 0}$

と表現します．この方程式を満たす， $\displaystyle{ x }$ を近似的に求めていきます．

ここで，このニュートン法の理解のコツとして，図を用いて説明していきます．この $\displaystyle{ f(x) }$ を関数として，

$\displaystyle{ y = f(x) }$

と考えると，求める解は以下の図の $\displaystyle{ y = f(x) = 0}$ を満たす点，つまり，軸との交点ということがわかります．

f:id:ReK2Science:20201003165241p:plain

では，具体的な手順を見ていきます．

初期値 $\displaystyle{ x^{(0)} }$ の点で垂線を引きます．この $\displaystyle{ x^{(k)} }$ は，微分や累乗を表しているのでなく，ｋ回目の計算で求めた解という意味で，第ｋ次近似解とか言われます．この初期値 $\displaystyle{ x^{(0)} }$ は，適当に決めます．大体の場合は，どんな値にしても最終的にはうまくいきます．
曲線 $\displaystyle{ f(x) }$ との交点をAとします．
A点での接線の方程式を立てます．
$\displaystyle{ y - f(x^{(0)} )= f'(x^{(0)}) ( x - x^{(0)}) }$

より

$\displaystyle{ y = f'(x^{(0)}) ( x - x^{(0)}) + f(x^{(0)} ) }$
その接線と水平軸との交点をBとし，座標値 $\displaystyle{ x^{(1)} }$ とおきます

上の接線の式より次のように求まります．

$\displaystyle{ 0 = f'(x^{(0)}) ( x - x^{(0)}) + f(x^{(0)} ) }$
線の方程式を立てます．
$\displaystyle{ x^{(1)} = x^{(0)} - \frac{f(x^{(0)})}{f'(x^{(0)})} }$
この操作を繰り返す．
一般に， $\displaystyle{ x^{(k+1)} }$ は次のように表せます．
$\displaystyle{ x^{(k+1)} = x^{(k)} - \frac{f(x^{(k)})}{f'(x^{(k)})} }$
操作を繰り返すにつれて， $\displaystyle{ x^{(k+1)} }$ は限りなく $\displaystyle{ f(x) = 0}$ の解に近づいていきます．

以上です！こんな手順です！

手順はわかったけど，まだなんかしっくりこないなあ，，，って人が多いと思います．

それは当然で，実際にこれを利用した具体例がないとイメージがわかないと思います．

計算例

具体例を，計算してみましょう．

$\displaystyle{ x^{2} = 3 }$ をニュートン法で解け．

この問題は，別に数値解析でなくても解けますね．この解は，

$\displaystyle{ x = \pm{\sqrt{3}} }$

ですね！だいたい，1.7320508・・・（ひとなみにおごれや）ですね．

では，これを，ニュートン法を用いて解いたとき，どうなるか見ていきましょう．

まず，次のように変形します．

$\displaystyle{ f(x) = x^{2} - 3 = 0 }$

この時，以下のように計算できます．

$\displaystyle{ f'(x) = 2 x }$

これらを用いて，以下のようにニュートン法の計算を行います．

$\displaystyle{ x^{(k+1)} = x^{(k)} - \frac{ (x^{(k)})^{2} - 3 }{ 2 x^{(k)} } }$

となります．ちなみにですが，私の場合以下のように変形します．計算ミスを減らすためです．累乗の計算をしなくて済みます．

$\displaystyle{ x^{(k+1)} = \frac{ 1 }{ 2 } ( x^{(k)} + \frac{ 3 }{ x^{(k)} } ) }$

では，さっそく計算してみましょう．ここでは，初期値を $\displaystyle{ x^{(0)} = 2.0 }$ とします．

\begin{eqnarray} x^{(1)} &=& \frac{ 1 }{ 2 } ( x^{(0)} + \frac{ 3 }{ x^{(0)} } ) \\ &=& \frac{ 1 }{ 2 } ( 2 + \frac{ 3 }{ 2 } ) \\ &=& 1.75 \end{eqnarray}

次も行きます！

\begin{eqnarray} x^{(2)} &=& \frac{ 1 }{ 2 } ( x^{(1)} + \frac{ 3 }{ x^{(1)} } ) \\ &=& \frac{ 1 }{ 2 } ( 1.75 + \frac{ 3 }{ 1.75 } ) \\ &=& 1.732142857 \end{eqnarray}

\begin{eqnarray} x^{(3)} &=& \frac{ 1 }{ 2 } ( x^{(2)} + \frac{ 3 }{ x^{(2)} } ) \\ &=& \frac{ 1 }{ 2 } ( 1.732142857 + \frac{ 3 }{ 1.732142857 } ) \\ &=& 1.73205081\end{eqnarray}

以上です！だいぶ， $\displaystyle{ \sqrt{3} }$ に近い値が計算で求まってきましたね！これをずっと繰り返すと，さらに精度が高まってきます！

ですが，ここで，気づいてほしい問題が2つあります．

1つ目は，もう一つの解の $\displaystyle{ - \sqrt{3} }$ の結果が得られなかったこと.ちなみに今回も含め，大体の場合，初期値の与え方で，ほかの解も得られます．

2つ目は，初期値を $\displaystyle{ x^{(0)} = 0.0 }$ とすると，分母がゼロとなり，計算ができないこと．

おわりに

いかがでしたか?

もし，どうしても解けない方程式があなたの目の前に現れても，あっても今日の方法を使えば，何とか太刀打ちできます．

次回は，ニュートン法での方程式の解法を，本格的にC言語でコンピュータでの計算を詳しく行っていきましょう！

www.rek2u.com

本日も、りけいのりがお届けしました。

参考文献

1)高橋麻奈『やさしいC　第4版』　風工舎

www.amazon.co.jp

2)安田仁彦『数値解析基礎』　コロナ社

www.amazon.co.jp

2020-12-20

【プログラミング】Visual Studio 2019でのプロジェクトの作成・実行

プログラミング

本日も、りけいのりからお届けします。

今回は， Visual Studio 2019 でのコンソールアプリケーション開発手順を説明していきます．

コンソールアプリケーションって？？

と思ったと思います．コンソールアプリケーションはWindowsのコマンドプロンプトで実行されるプログラムのことです．この記事で行う数値解析での，プログラムはこのコンソールアプリケーションで問題なく行えます．

この Visual Studio のインストールは過去記事と以下のリンクを参照してください．

visualstudio.microsoft.com

f:id:ReK2Science:20201004193035p:plain

（１）Visual Studioの起動
（２）プロジェクトの作成
（４）ソースファイルの登録
（５）ソースコード入力
（６）実行
おわりに
- 参考文献

（１）Visual Studioの起動

これは，簡単ですね．ここでは，スタートボタンから検索してみました．

f:id:ReK2Science:20200925225753j:plain — 図１

起動すると，図２のようなスタートページが開きます．

f:id:ReK2Science:20200925230119j:plain — 図２

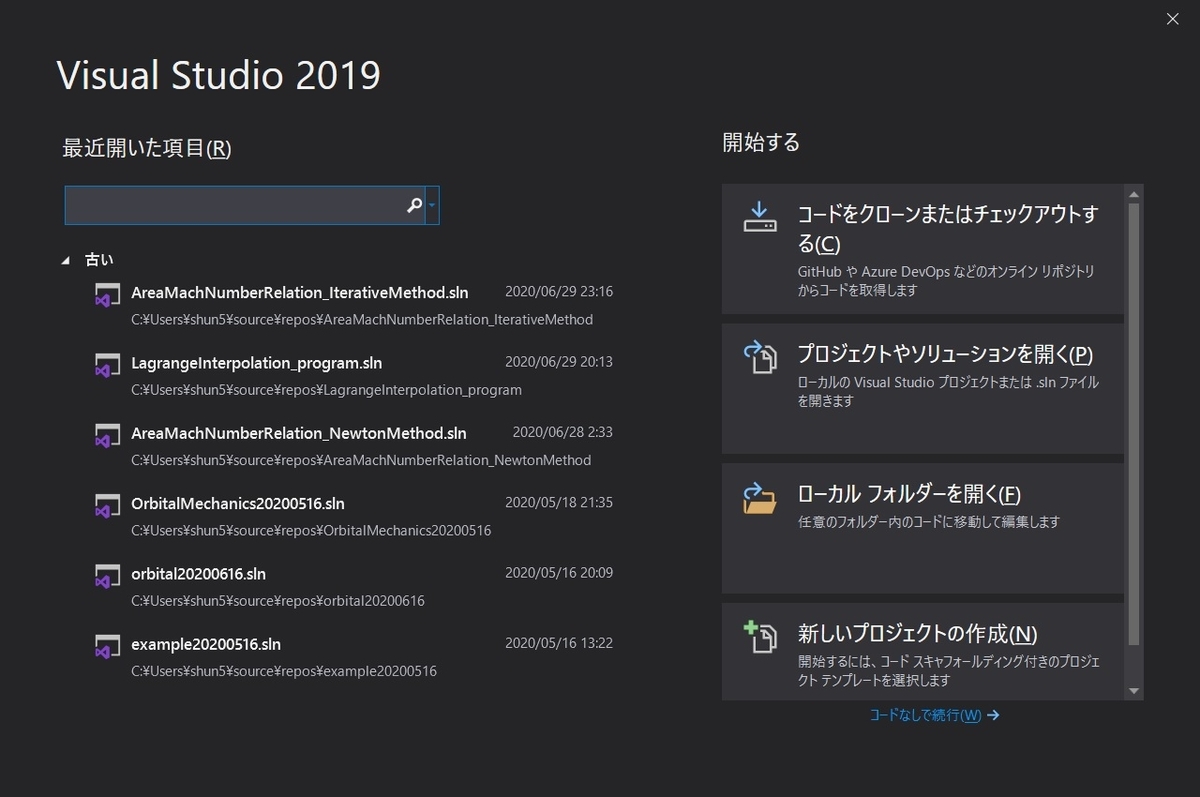
（２）プロジェクトの作成

今回は，新しいプロジェクトを作成するので，図２のスタートページの

新しいプロジェクトの作成(N)

を選択し，「次へ」をクリックすると，図３のような画面になります．

f:id:ReK2Science:20200925231011j:plain — 図３

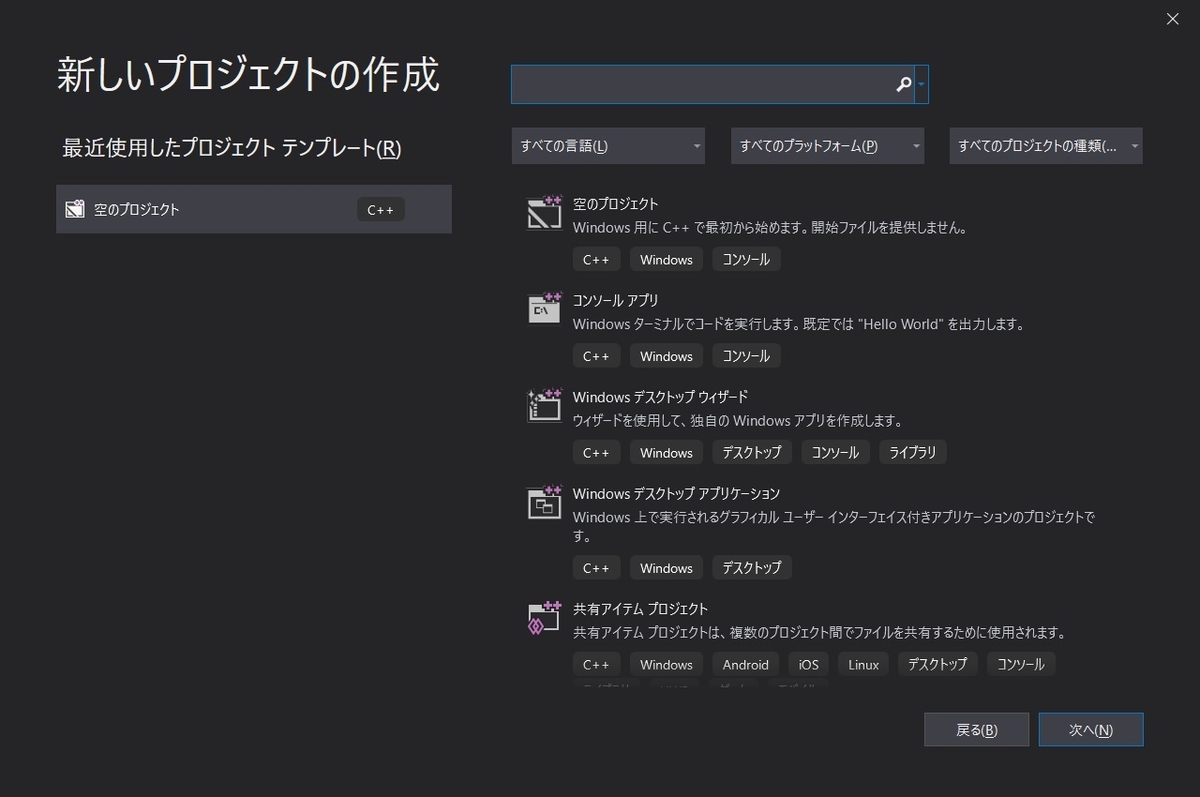
ここでは，

空のプロジェクト

を選択します．すると，図４のような画面になります．

f:id:ReK2Science:20200925231107j:plain — 図4

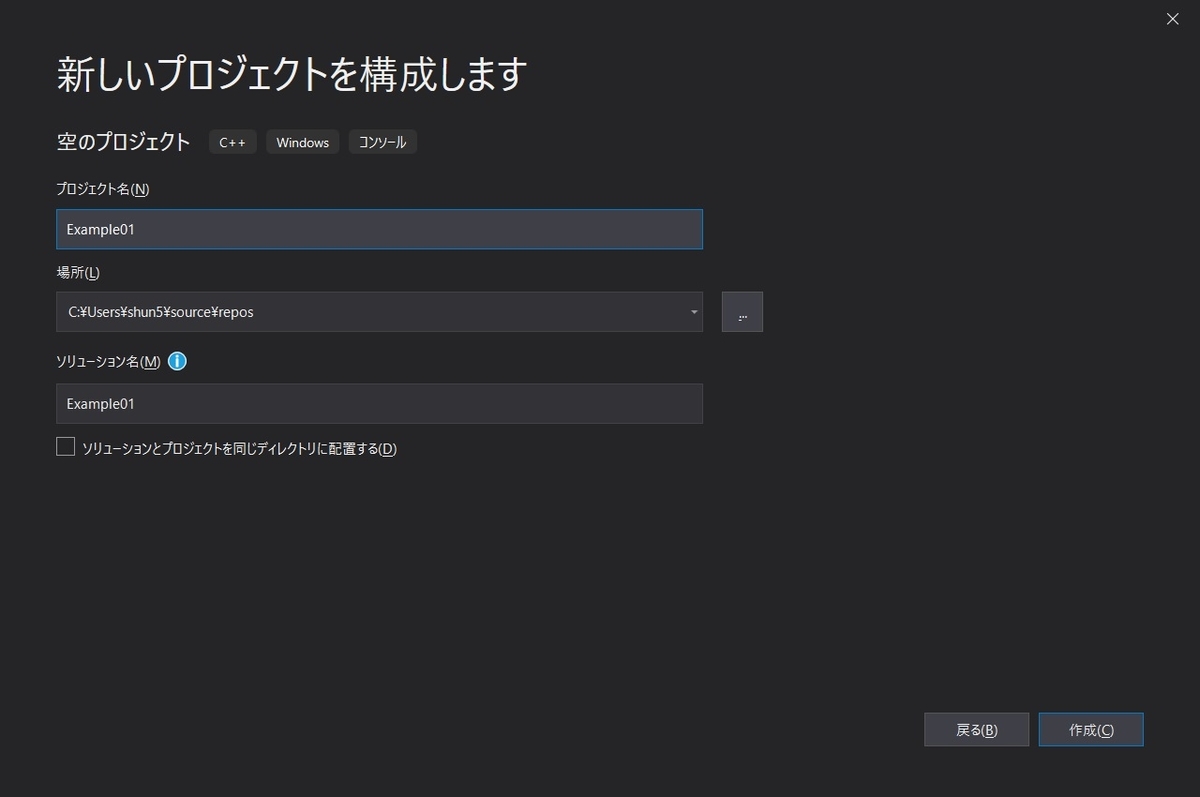
ここでは，以下の操作を行います．

プロジェクト名(N)
任意に設定
（例）Example01
場所(L)
任意に設定できるが，そのままでもよい
ソリューションとプロジェクトを同じディレクトリに配置する(D)
チェックマークを外す

そして，「作成」をクリックすると，図５のように設定が完了し画面が切り替わります．

f:id:ReK2Science:20200925233454j:plain — 図５

今回は，コンソール画面の出力設定をします．実行結果をコマンドプロンプトで表示できるようにします．この設定は，初回の一回のみで大丈夫です．

f:id:ReK2Science:20200925233844j:plain — 図６

まず，図５の画面のプルダウンメニューから，図6のように

プロジェクト(P)　＞　プロパティ(E)

と選択します．すると図7のような画面が表示されます．

f:id:ReK2Science:20200925233917j:plain — 図７

まず，画面左端の縦長の欄において

リンカー　＞　システム

を選択します．次に右側の欄の

サブシステム　＞　コンソール(SUBSYSTEM・・・)

を選択し，「OK」をクリックすると，図８のような画面に戻ってきます．

これにて，「コンソール」の設定が完了しました．

（４）ソースファイルの登録

f:id:ReK2Science:20200926000020j:plain — 図９

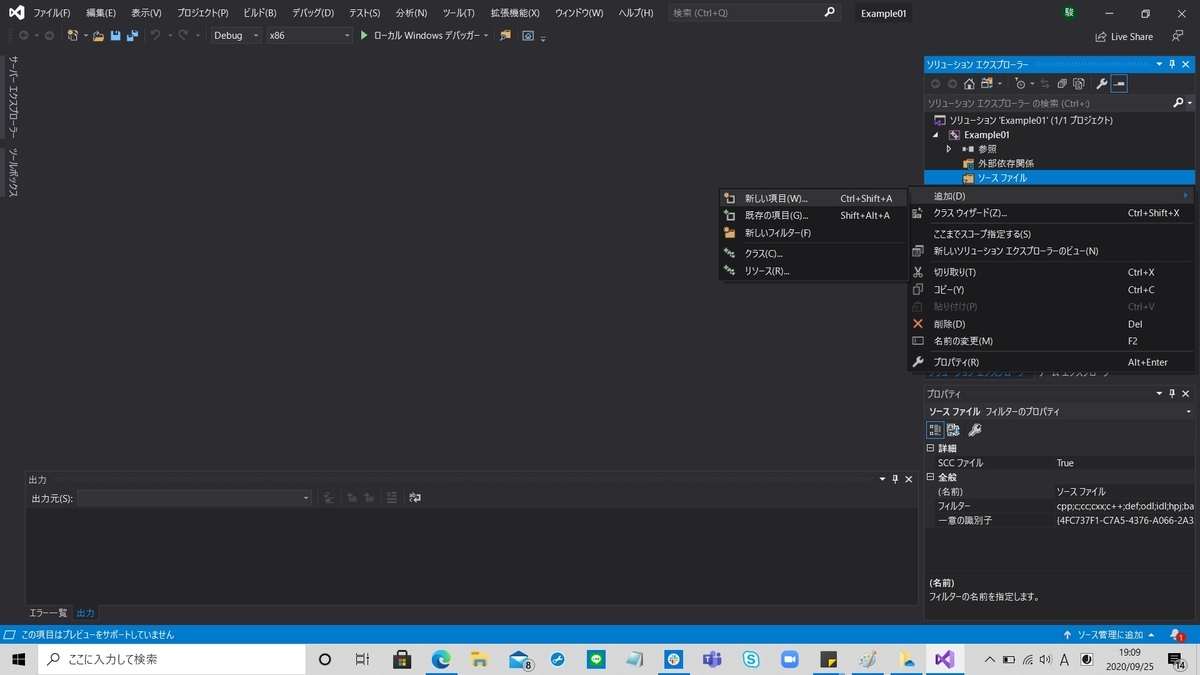
図９のように，画面右側のソリューションエクスプローラーの

ソースファイル

を右クリックし，

追加(D)　＞　新しい項目(W)

と選択します．すると図10のような画面が表示されます．

f:id:ReK2Science:20200926000141j:plain — 図10

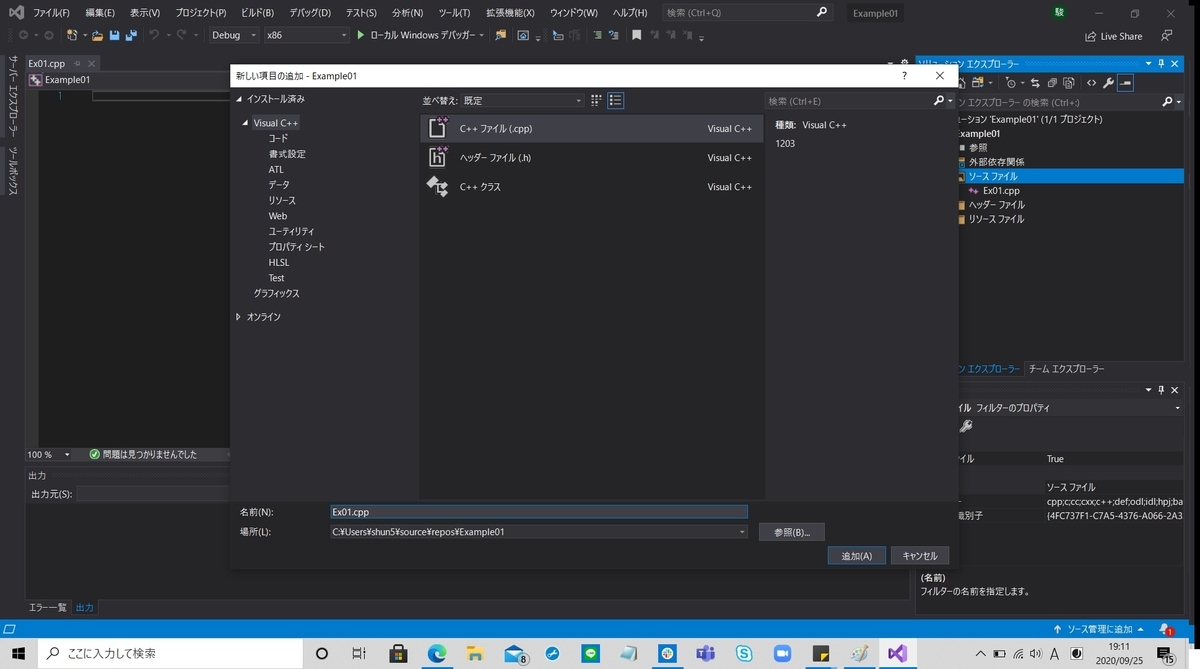
ここでは，以下の操作を行います．

「C++ファイル (.cpp)」を選択

名前(N)
任意に設定
（例）Ex01 　（拡張子.cpp　が自動でつきます．）
場所(L)
任意に設定できるが，そのままでもよい

そして，「追加」をクリックすると，図１１のように設定が完了し画面が切り替わります．

f:id:ReK2Science:20200926000644j:plain — 図１１

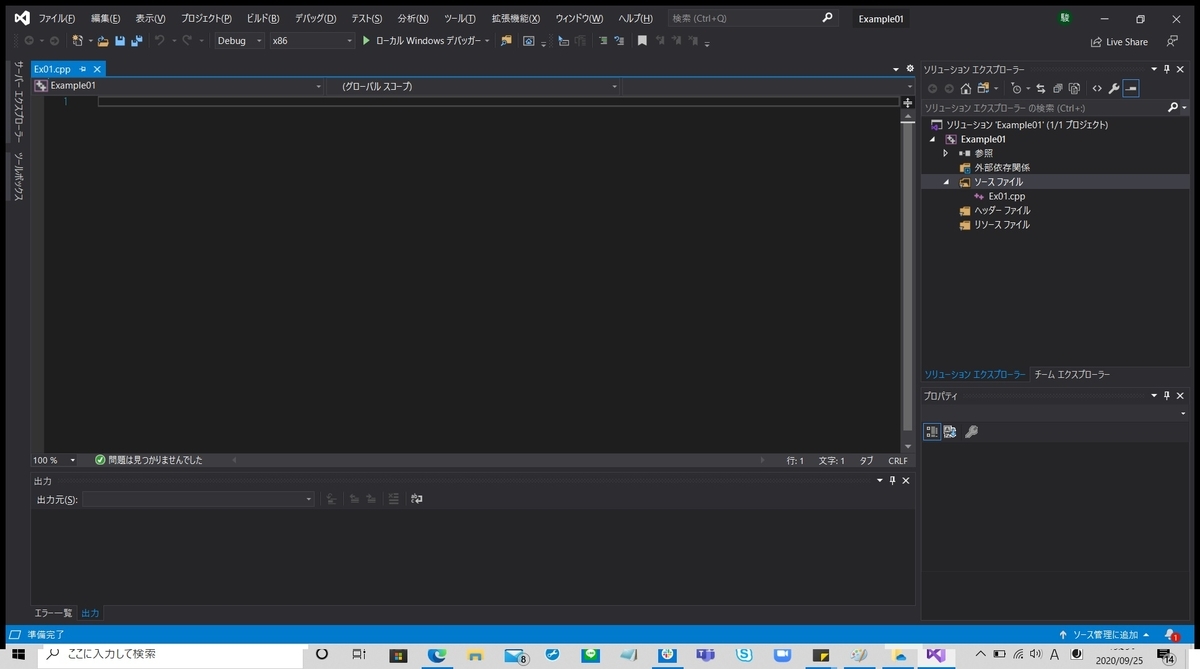
この操作によって，図９の画面から，図11のように，編集画面（エディタ）が表示されます．そして，ここに，ソースコードを入力していきます．

（５）ソースコード入力

f:id:ReK2Science:20200926002018j:plain — 図12

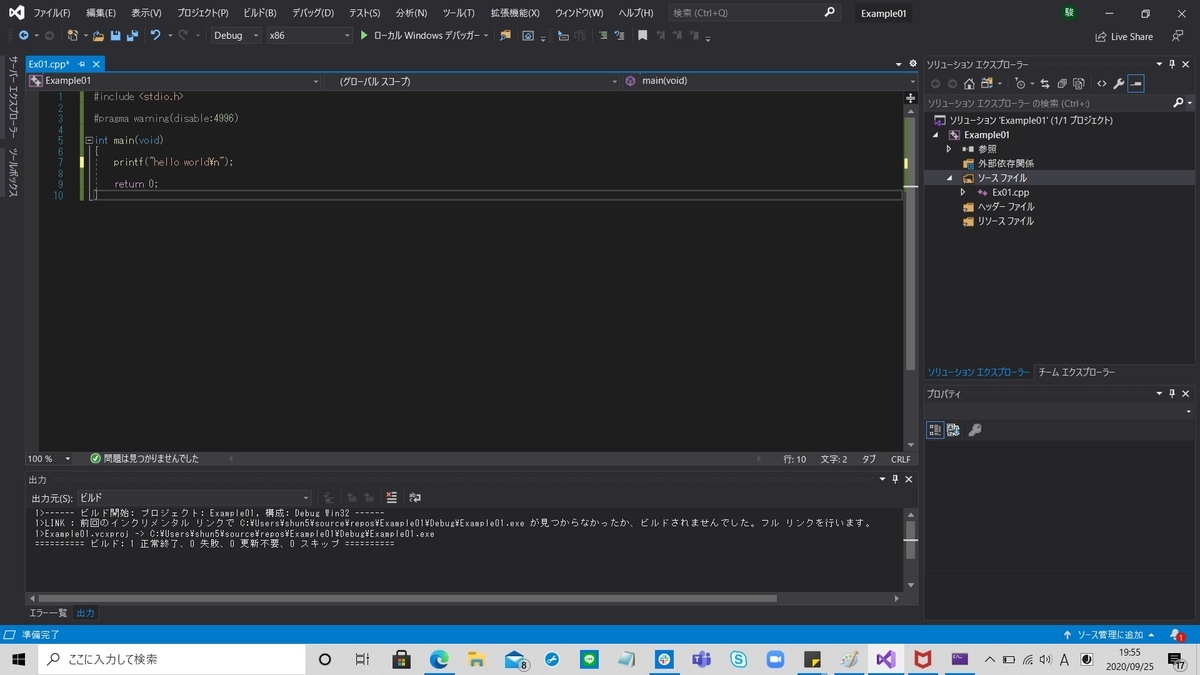
図12のようにソースコードを記述します．今回は，以下のソースコードを入力しました．

ソースコード

#include <stdio.h>
#pragma warning(disable:4996)

int main(void)
{
printf("hello world\n");
return 0;
}

このソースコードは

画面に「hello world」という文字を出力せよ！

っという処理です．

前回も書きましたが，慣例的に，プログラム初心者が始めてプログラミングで画面出力を行うとき，新しい開発環境でプログラミングを試してみるとき，新しく開発した画面出力のデバイスの試験では，この「hello world」の文字が多用されます．

日本の無線で言うところの，「本日は晴天なり　本日は晴天なり」と同じようなものですね．

だからこそ，先ほどのソースコードのことを，私の先生は「世界で最も書かれているソースコードである」と言っていました．

（６）実行

ソースコードの入力が完了したらファイルを保存し，ビルドを行い一気に実行を行います．このビルドは，コンパイルとリンクのことです．

図12のメインメニューから

デバック(D)　＞　デバックなしで開始(H)

と選択します．すると図1３のように，コマンドプロンプトが起動し，実行結果が出力されます．

f:id:ReK2Science:20200925200809j:plain — 図13

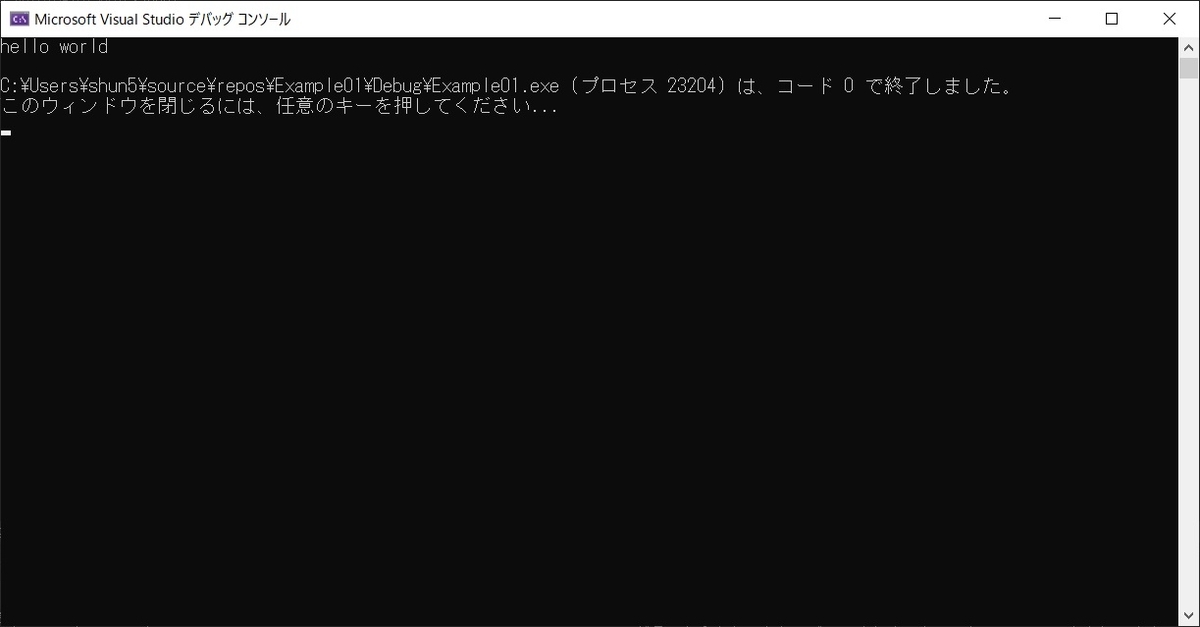
このように，「hello world」の文字が出力されていますね．

おわりに

いかがでしたか?

今回は，Visual Studio 2019でのプロジェクトの作成・実行を具体的に行ってみました．

何かソースコードが作成できましたら，この記事の手順でやってみてください．

次回は，ようやく，数値解析を行って，方程式を解いてみようと思います．

▽前回の記事も併せてお読みください!!▽

www.rek2u.com

本日も、りけいのりがお届けしました。

参考文献

1)高橋麻奈『やさしいC　第4版』　風工舎

www.amazon.co.jp

2)安田仁彦『数値解析基礎』　コロナ社

www.amazon.co.jp

2020-12-19

【プログラミング】作成から実行までの流れ

プログラミング

本日も、りけいのりからお届けします。

前回の記事で，なんとなく，プログラミングのイメージは，

「プログラム」は，コンピュータに対してなんらかの「仕事」を指示するためのもの

「プログラミング」はその「プログラム」を作ったり実行すること

としましたね．それで，今回は，もっと詳しくプログラミングの流れと，プログラムで使用するソフトウェアのVisual Studio Communityの説明を行っていきます．

f:id:ReK2Science:20201004193114p:plain

プログラミングの作成
プログラミング勉強の進め方！
Visual Studio Communityのインストール
おわりに
- 参考文献

プログラミングの作成

プログラムを実行する際の流れを説明します．

プログラムを作成するとき，ソースコードを書きます.例えば，こんな感じです．

ソースコード

#include <stdio.h>
#pragma warning(disable:4996)

int main(void)
{
printf("hello world\n");
return 0;
}

このソースコードは

画面に「hello world」という文字を出力せよ！

っという処理です．今回はC言語で記述しました．このコードを保存したファイルをソースファイルといいます．

このソースコードを作成することがプログラミングで行う主の作業です．世界中のプログラマーはこのソースコードの作成をずっとやっています．そして，このソースコードの記述の決まり―文法―を勉強していきます！これが，プログラミングの勉強です．この文法をマスターしていくことで，自分の書きたいソースコードをかけるようになっていきます．

ですが，ソースコードを書くだけでは，プログラミングは実行できません．

次は，人間が記述したソースコードを機械が理解することのできる機械語に変換する作業のコンパイルを行います．

機械語は，０と1のみで記述されています．とても人が読むことは困難です．しかし，機械（コンピュータ）は機械語しか理解できません．

この変換に用いるソフトウェアをコンパイラと呼びます．

そして，最後にコンピュータがその機械語を理解して，プログラムを実行してくれます．先ほどのソースコードは次のように実行されました．

f:id:ReK2Science:20200925195659j:plain

余談ですが，この「hello world」ってなんだろう，，，と思った人もいると思います．

別に，この出力させる文字は何だってかまいません．「hello world」でなくても，「hello!」「Hi」「こんにちは」「OK！」でも，なんだっていいです．しかし，慣例的に，プログラム初心者が始めてプログラミングで画面出力を行うとき，新しい開発環境でプログラミングを試してみるとき，新しく開発した画面出力のデバイスの試験では，この「hello world」の文字が多用されます．

日本の無線で言うところの，「本日は晴天なり　本日は晴天なり」と同じようなものですね．

だからこそ，先ほどのソースコードのことを，私の先生は「世界で最も書かれているソースコードである」と言っていました．

話を戻して，このプログラムの実行の流れを以下の図にまとめました．

f:id:ReK2Science:20201001225139p:plain

しかし，この記事では，コンパイルやリンクをそこまで，意識する必要はありません．この記事で使用するソフトウェアのVisual Studio Communityは総合開発環境と呼ばれます．ふつうは，ソースコードの記述や，コンパイルは別々のソフトウェアで行っていましたが，総合開発環境では，すべて一つのソフトウェアでプログラミングを実行することができます．

プログラミング勉強の進め方！

繰り返しになりますが，プログラムの勉強は，ソースコードの記述の決まり―文法―の勉強です！この記事では，そのソースコードを記述する言語としてC言語を採用し，数値解析とC言語の文法についてをメインで連載します．

そして，この記事の一番の特徴としまして，実際の数値解析に用いたプログラムを用いて，C言語の文法の解説をしていきます．つまり，通常の学習手順と逆です！

通常：　C言語の文法の基礎を勉強　→　数値解析などへ応用

今回：　数値解析のプログラム　→　そこから細かく文法を解析

このため，C言語の文法の基礎については，少し浅い説明なってしまうかもしれません．しかし，プログラミングを用いた数値解析のイメージや，プログラムの応用はとても分かりやすく理解できると思います．

また，ここではできるだけ，多くの図解を用いてわかりやすく説明していきます．コンピュータの中で起こっていることでも，イメージを図にすることで理解が深まるのはよくあります．

自分にC言語を教えてくれた先生は，「独学でプログラムを勉強する場合，ポインタまでいければいいほう」と言っていました．この先生の時代と，インターネットが普及し，様々な情報が簡単に見れる今の時代は違うと思いますが，プログラミングをしていると，ソースコードのミスや実行でのエラーは日常茶飯事です．だからこそ，自分でミスを見つけることも大切ですが，人に頼ることで問題がすぐ解決することはよくあります．幸い，今はインターネットで，たくさんの人がプログラムのエラーの説明や対処をまとめてくれています．そのさまざまな情報をぜひ生かして，勉強していきましょう！

Visual Studio Communityのインストール

では，さっそく始めていきましょう！Visual Stdio Communityは以下のサイトよりインストールできます．Visual Stdio Communityは無料で使うことができます！

visualstudio.microsoft.com

ちなみに，インストールは結構時間がかかります．．．．

このインストールの最中にも，何点か設定が必要になります．

おわりに

いかがでしたか?

今回は，ざっくりと，プログラミングの流れを説明していきました．次回は，実際に，Visual Studio Communityでのプログラムの作成から実行までの具ライ的な流れを追っていきましょう！

www.rek2u.com

本日も、りけいのりがお届けしました。

参考文献

1)高橋麻奈『やさしいC　第4版』　風工舎

www.amazon.co.jp

2)安田仁彦『数値解析基礎』　コロナ社

www.amazon.co.jp

2020-12-18

【プログラミング】Introduction

プログラミング

本日も、りけいのりからお届けします。

今回からは、新しいカテゴリーであるプログラミングについての記事を連載します。

皆さん，プログラミングと聞いたらどのようなイメージを持つでしょうか？

ホームページ作成，アプリ開発，，，，，

ですが，今回はプログラミングで計算する！ということをテーマにして記事を連載してきます！そのため，

まず，この連載は

・プログラミングに興味がるけど何から始めればよく分からない人

・プログラミングを用いた数値解析・画像処理をしてみたい人

・とても解けないような計算を解く必要がある人

・プログラミングの授業の課題中に壁にぶつかった人

を対象しています！

また．ここでは，学生向けの無料のVisual Studio Communityというソフトウェアを用いてプログラミングを行います！必要なものは，パソコンだけです！

f:id:ReK2Science:20200919023135j:plain

プログラミングってそもそも何だろう？
数値解析とは
おわりに
- 参考文献

プログラミングってそもそも何だろう？

昔，私は塾講師のアルバイトをしていました．その勤務先の塾では，私が勤務している間に，小学生を対象としたプログラミング教室が開講しました．小学生の習い事の一つが，プログラミングというのが当たり前になりつつあることに驚いたのを覚えています．

話を戻して，そもそものプログラミングとかプログラムについて考えていきたいと思います．参考文献の安田仁彦先生の『数値解析法』の記述を読んでいきましょう．

一連の計算を行うための計算手順をアルゴリズム(algorithm)という．このアルゴリズムに従ってコンピュータに計算を行わせるため，コンピュータが理解できる言語を用いてアルゴリズムを具体的に記述したものをプログラム(program)という．

次に，同じく参考文献の高橋麻奈先生の『やさしいC　第4版』の記述を読んでいきましょう．

私たちは毎日，コンピュータにインストールされたワープロ，表計算ソフトなど，さまざまな「プログラム」を使っています．ワープロのような「プログラム」を使うということは，

文字を表示し，書式を整え，印刷する

といった特定の「仕事」をコンピュータに指示し，処理させていると考えることもできます．

コンピュータは，さまざまな「仕事」を正確に，速く処理できる機械です．「プログラム」は，コンピュータに対してなんらかの「仕事」を指示するためのものです．

ということです．これは，プログラムに限った話ではないですが，タイプの違う別々の教科書で同じ事柄について書かれている部分を読み比べることは，より理解を深めることができる場合がありますよね．

話を戻しまして，プログラミングについて，個人的には，かなりゆるく，

「プログラム」は，コンピュータに対してなんらかの「仕事」を指示するためのもの

「プログラミング」はその「プログラム」を作ったり実行すること

というイメージで考えています．たぶん，最初はこのくらいのイメージで勉強を始めても大丈夫だと思います．

数値解析とは

ここでは，数値解析の例から，プログラミングを用いて計算を行う例を示します．

皆さん，以下の式を解いてみましょう！

$\displaystyle{ 8x + 4 = 36 }$

中学校一年生の一次方程式の問題ですね．答えは次のようになりますね．

$\displaystyle{ x = 4 }$

では，次の問題も見ていきましょう．

$\displaystyle{ \sqrt{3} cos x + sin x = 2 }$

高校の三角方程式の問題です．加法定理を用いてとけそうですね．範囲を $\displaystyle{ 0 \leq x \leq \frac{ \pi }{ 2 }}$ ととると，こうなりますね．

$\displaystyle{ x = \frac{ \pi }{ 6 } }$

では，最後にこの問題を見ていきましょう． $\displaystyle{E_0}$ ， $\displaystyle{e}$ ， $\displaystyle{t_0}$ ， $\displaystyle{t}$ が定まった時， $\displaystyle{E}$ を求めます．

$\displaystyle{ E - e sin E - ( E_0 - e sin E_0 ) = n ( t - t_0 ) }$

文字が多くて，ややこしいですが，これも一次方程式なのでうまい変形をしたら解けそうですよね．しかし，この方程式は解けません．ちなみに，この方程式は，ケプラーの法則から求められる式で，地球の軌道上の人工衛星の時間と場所を関係づける式です．

このように，未知数が，たった一つである一次方程式でさえ，場合によっては解くことができません．工学の分野では，このような簡単には解くことができない方程式や，積分の計算，数値の補間によく出会います．こんな時こそ，コンピュータでプログラミングを用いて計算して解きます！

おわりに

いかがでしたか?

実をいうと，この記事の執筆者もプログラムに詳し訳ではなく，専門は別分野で，プログラムを用いて計算する人間です！そのため，もしかしたら，用語の説明などでは，間違っていることがあるかもしれません．すみません．．．．

しかし，ここ記事のテーマは，プログラミングで計算する！です．

なので，とにかく，使うということに重点を置いて説明していきたいと思います！

次回は，プログラミングの流れの説明とこの記事で使用するソフトウェアについて説明しいきます！

本日も、りけいのりがお届けしました。

参考文献

1)高橋麻奈『やさしいC　第4版』　風工舎

www.amazon.co.jp 2)安田仁彦『数値解析基礎』　コロナ社

www.amazon.co.jp

2020-12-13

【応用数学】知っといてほしい用語と基本【微分方程式③】

数学

本日も、りけいのりからお届けします。

今までは，微分方程式のイメージをつかむのが目的でした．

今回から，ようやく微分方程式の解法に入っていきます．

まずは，準備段階です．

紹介の前に知っておいてほしい語句や，解法に必要な数学の基本などを紹介します．

何度も繰り返しですが，ここでは，工学などへの応用を前提として，どうやって解くかに焦点を当てます．

f:id:ReK2Science:20201001223519p:plain

知っておいてほしい微分方程式の基本
微分方程式の解法って？
微分方程式の種類
微分方程式の例１：力学（質点の落下）
微分方程式の例２：力学（空気抵抗を受ける物体の落下）
おわりに
参考文献

知っておいてほしい微分方程式の基本

語句
語句を知っていると，たぶんこれからの説明がすんなり入ってくると思います．
微分方程式の解法：微分方程式の形によって毎回異なる解法をする！
ｎ階微分方程式の一般解は，ｎ個の任意定数を含む

ぶっちゃけ，今回の記事で一番言いたいことはこれです．

詳しく見ていきましょう

ある独立変数 $\displaystyle{x }$ に対する未知関数 $\displaystyle{ y = f(x) }$ が導関数 $\displaystyle{ \frac{dy}{dx} }$ を含む方程式を微分方程式と呼ぶ．

そして，微分方程式を満足し，独立変数 $\displaystyle{x }$ に対する未知関数 $\displaystyle{ y = f(x) }$ を，導関数 $\displaystyle{ \frac{dy}{dx} }$ を含まない関係式へ導くことを，微分方程式を解くという．

よくわかりませんね．

そこで，以下の例題から，説明していきます．

繰り返しになりますが，今回は用語の詳しい説明はせず紹介のみです！次回以降に詳しく説明します．ここでは，ぜひ，「微分方程式のイメージ」をつかんでみてください！

微分方程式の解法って？

では，見ていきましょう！

それと，普通の教科書の微分方程式の分類は，線形かどうかとか，斉次かどうかとか，何階かみたく分類してあると思います．しかし，ここでは，解ける形ごとに分けて分類しています．

変数分離形
定数変化法を行う変数分離形
同次形微分方程式
ベルヌーイの微分方程式
完全微分方程式
非線形の微分方程式（TypeA)
非線形の微分方程式（TypeB)
非線形の微分方程式（TypeC)
定数係数線形微分方程式
非斉次の定数係数線形微分方程式
オイラーの微分方程式

連立微分方程式とかもありますが，なんか少し違いうのでこの分類には入れませんでした．

微分方程式の種類

では，見ていきましょう！

変数分離形
定数変化法を行う変数分離形
同次形微分方程式
ベルヌーイの微分方程式
完全微分方程式
非線形の微分方程式（TypeA)
非線形の微分方程式（TypeB)
非線形の微分方程式（TypeC)
定数係数線形微分方程式
非斉次の定数係数線形微分方程式
オイラーの微分方程式

連立微分方程式とかもありますが，なんか少し違うのでこの分類には入れませんでした．

微分方程式の例１：力学（質点の落下）

地上から，初速度 $\displaystyle{v_0}$ で質点 $\displaystyle{m}$ を鉛直上向きに投げ上げるとする．地面から鉛直上向きを $\displaystyle{x}$ 軸としたとき，時間 $\displaystyle{t}$ に対する質点の変位 $\displaystyle{x}$ を求めよ．またこの時，重力加速度を $\displaystyle{g}$ ，地面を $\displaystyle{ x=0 }$ ，投げ上げた瞬間の時間を $\displaystyle{ t=0 }$ とする．

まず，この時初期条件は以下のようになります．

$\displaystyle{ t = 0 }$ の時， $\displaystyle{ v = v_0 }$ , $\displaystyle{ x = 0 }$

次に，質点に働く力は重力のみです．よって以下の図のようになります．

f:id:ReK2Science:20200926232127p:plain — 質点の落下

ここで，変位 $\displaystyle{x}$ と速度 $\displaystyle{v}$ と加速度 $\displaystyle{a}$ にはつぎのような関係があります．

$\displaystyle{ a = \frac{dv}{dt} = \frac{d^2x}{dt^2} }$

$\displaystyle{ v = \frac{dx}{dt} }$

よって，運動方程式が次のようになります．

$\displaystyle{ m \frac{d^2x}{dt^2} = -mg }$

これが，いわゆる微分方程式です．次にこの微分方程式を解いていきます．

まずは，速度 $\displaystyle{v}$ を利用して

$\displaystyle{ m \frac{dv}{dt} = -mg }$

このように，微分方程式を書き直します．

ここで，両辺を独立変数 $\displaystyle{t}$ で積分します．このとき，不定積分なので，積分定数 $\displaystyle{A}$ が出てきます．

$\displaystyle{ \int m \frac{dv}{dt} dt　 \ = - \int mg dt　 \ + A }$

$\displaystyle{ v = -gt + A }$

よって，速度について解くことができました！さらに解法を続けます．まず，速度 $\displaystyle{v}$ を変位 $\displaystyle{x}$ で置き換えます．

$\displaystyle{ \frac{dx}{dt} = -gt + A }$

同様に，両辺を独立変数 $\displaystyle{t}$ で積分します．この時，積分定数を $\displaystyle{B}$ とおきます．

$\displaystyle{ \int \frac{dx}{dt} dt　 \ = \int (-gt + A) dt　 \ + B }$

$\displaystyle{ x = -\frac{1}{2}gt^2 + At + B }$

よって，位置 $\displaystyle{x}$ について解くことができました！これが，一般解です．

そして，ここで，初期条件を用いて，積分定数 $\displaystyle{A}$ ， $\displaystyle{B}$ を定めていきましょう．

初期条件を用いて，求めた一般解に代入して解くと，

$\displaystyle{ A = v_0 }$

$\displaystyle{ B = 0 }$

このような結果になります．よって，これを一般解に代入すると，こうなります．

$\displaystyle{ x = -\frac{1}{2}gt^2 + v_0t }$

これは，特殊解と呼ばれます．

これで，問題が解けましたね！ちなみに，この解法は変数分離形と呼ばれます．

せっかくなので，速度 $\displaystyle{v}$ も求めてみましょう．

$\displaystyle{ v = -gt + v_0 }$

となります．ここで，時間 $\displaystyle{t}$ に対する速度 $\displaystyle{v}$ と変位 $\displaystyle{x}$ の変化をグラフに表してみます．

f:id:ReK2Science:20200926232804p:plain — 質点の落下における時間と変位の関係

f:id:ReK2Science:20200926233351p:plain — 質点の落下における時間と速度の関係

微分方程式を解き，一般解を求め，初期条件を利用して，特殊解を求めると，時間に対する質点の位置や速度が定まりましたね！

微分方程式の例２：力学（空気抵抗を受ける物体の落下）

地上から，初速度 $\displaystyle{v_0}$ で質点 $\displaystyle{m}$ を鉛直上向きに投げ上げるとする．また，物体は速度の２乗に比例して比例定数 $\displaystyle{c}$ の空気抵抗を受けるとする．地面から鉛直上向きを $\displaystyle{x}$ 軸としたとき，時間 $\displaystyle{t}$ に対する質点の速度 $\displaystyle{v}$ を求めよ．またこの時，重力加速度を $\displaystyle{g}$ ，地面を $\displaystyle{ x=0 }$ ，投げ上げた瞬間の時間を $\displaystyle{ t=0 }$ とする．

同様に解いていきます．

まず，初期条件は以下のようになります．

$\displaystyle{ t = 0 }$ の時， $\displaystyle{ v = v_0 }$ , $\displaystyle{ x = 0 }$

次に，質点に働く力は重力と空気抵抗です．よって以下の図のようになります．

f:id:ReK2Science:20200926233941p:plain — 空気抵抗を考慮した質点の落下

全問と同様に，変位 $\displaystyle{x}$ と速度 $\displaystyle{v}$ と加速度 $\displaystyle{a}$ にはつぎのような関係があります．

$\displaystyle{ a = \frac{dv}{dt} = \frac{d^2x}{dt^2} }$

$\displaystyle{ v = \frac{dx}{dt} }$

よって，運動方程式が次のようになります．

$\displaystyle{ m \frac{d^2x}{dt^2} = -mg -c(\frac{dx}{dt})^2}$

これが，同様に微分方程式です．次にこの微分方程式を解いていきます．

まずは，速度 $\displaystyle{v}$ を利用して

$\displaystyle{ m \frac{dv}{dt} = -mg -cv^2 }$

このように，微分方程式を書き直します．

ここで，この後の積分を考慮して変形します．この変形は，とにかく慣れです！たくさん練習して見極められるようになりましょう．イメージは左辺に未知関数を，右辺に独立関数を集めることです！

$\displaystyle{ \frac{m}{c} \frac{1}{ \frac{m}{c}g +v^2} \frac{dv}{dt} = -1 }$

両辺を独立変数 $\displaystyle{t}$ で積分します．このとき，積分定数を $\displaystyle{A}$ とします．

$\displaystyle{ \frac{m}{c} \int \frac{1}{ \frac{m}{c}g +v^2} \frac{dv}{dt} dt \ = - \int dt \ + A }$

$\displaystyle{ \frac{c}{m} Arctan\frac{c}{m}v= -t + A }$

$\displaystyle{ v=\frac{m}{c}tan(\frac{m}{c}(-t + A ))}$

よって，速度について解くことができました！さらに解放を続けます．まず，速度 $\displaystyle{v}$ を変位 $\displaystyle{x}$ で置き換えます．

$\displaystyle{ \frac{dx}{dt} = -gt + A }$

同様に，両辺を独立変数 $\displaystyle{t}$ で積分します．この時，積分定数を $\displaystyle{B}$ とおきます．

$\displaystyle{ \int \frac{dx}{dt} dt　 \ = \int (-gt + A) dt　 \ + B }$

$\displaystyle{ x = -\frac{1}{2}gt^2 + At + B }$

よって，位置 $\displaystyle{x}$ について解くことができました！これが，一般解です．

おわりに

いかがでしたか?

今回は，微分方程式のざっくりの説明と，物理の力学で応用されている微分方程式を例示しました．

しかし，世の中にはまだまだたくさんの微分方程式が存在します！

次回は，工学（電気回路・材料力学・機械力学）で応用されている微分方程式の具体例を紹介していきます

www.rek2u.com

本日も、りけいのりがお届けしました。

参考文献

１）矢野健太郎　石原繁　（1981），基礎解析学（改訂版）第38版，裳華房

２）高遠節夫　ほか　（2014），新応用数学　4版，大日本図書

３）馬場敬之　，スバラシク実力がつくと評判の力学キャンパス・ゼミ　改訂２，マセマ

４）西巻正郎　森武昭　荒井俊彦　（1990），電気回路の基礎（第三版），森北出版株式会社

５）西巻正郎　下川博文　奥村万規子　（1995），続　電気回路の基礎（第三版），森北出版株式会社

６）西村尚　（1988），ポイントを学ぶ材料力学（第36版），丸善出版

７）西村尚　（2004），機械力学（第12版），コロナ社

2020-12-12

【応用数学】微分方程式の応用例：工学編【微分方程式②】

数学

本日も、りけいのりからお届けします。

前回に続き，今回も微分方程式の応用例を紹介していきます．

今回は，工学（電気回路・材料力学・機械力学）で応用されている微分方程式の具体例を紹介していきます

今回も目標は，

「微分方程式のイメージがつかめた気がする！！」

「微分方程式ってこういう場面で使うんだ！！」

となることです．

f:id:ReK2Science:20201001223959p:plain

微分方程式の例３：電気回路（RLC回路）
微分方程式の例４：材料力学（たわみの微分方程式）
微分方程式の例５：機械力学（1自由度系）
おわりに
参考文献

微分方程式の例３：電気回路（RLC回路）

以下のような電気回路があるとする．時間 $\displaystyle{t}$ に対する入力電圧を $\displaystyle{e(t)}$ ，流れる電流を $\displaystyle{i(t)}$ とする．

f:id:ReK2Science:20201002181412p:plain

この時に，以下の関係があります．

$\displaystyle{ e(t) = Ri(t) + L\frac{di(t)}{dt} +\frac{1}{C}\int i(t) dt }$

この解法は，省略しますが，過渡応答や伝送回路の授業で計算することがあると思います．また普通の電気回路では，正弦波交流での三角関数の加減算の計算が難解なので，よく複素数を応用しますね！

微分方程式の例４：材料力学（たわみの微分方程式）

以下のように，ヤング率 $\displaystyle{E}$ ，断面2次モーメント $\displaystyle{I}$ ，長さ $\displaystyle{l}$ の片持ちばりがあります．自由端に集中荷重 $\displaystyle{W}$ が作用するとする．

f:id:ReK2Science:20201002181336p:plain — 荷重によるたわみ

このとき，はりの断面に作用する曲げモーメント $\displaystyle{M(x)}$ は，

$\displaystyle{ M(x) = -Wx }$

と表せる．この時たわみ $\displaystyle{v}$ は，

$\displaystyle{ \frac{d^2v}{dx^2} = -\frac{M(x)}{EI} = -\frac{W}{EI}x }$

と表せます．この式は，たわみの微分方程式と呼ばれます．この解法は，二階積分していく簡単に解くことができます！この場合，境界条件は，

$\displaystyle{ x = l }$ の時， $\displaystyle{ v = 0 }$ , $\displaystyle{ \frac{dv}{dx} = 0 }$

となりますので，たわみ $\displaystyle{v}$ は，

$\displaystyle{ v = \frac{W}{6EI}(x^3 -3l^2x +2l^3) }$

となります．さらに，たわみの最大 $\displaystyle{v_max}$ は，自由端の $\displaystyle{ x = 0 }$ に生じるので，

$\displaystyle{ v_max = \frac{Wl^3}{3EI} }$

となります．

この式により，はりに荷重が加わるときのたわみを解くことができます！

※初期条件と境界条件

この問題では，「初期条件」ではなく，「境界条件」という言葉を使っています．両方，微分方程式を解くうえでは，一般解から特殊解を求める際に利用します．しかし，工学上は，時間に対する条件なのか，空間に対する条件なのか，で使い分けがあるそうです．

微分方程式の例５：機械力学（1自由度系）

振動の解析では，振動系のモデル化から，運動方程式の導出・解法を行います．以下の図は，ばねとダンパによる1自由度系と呼ばれます．

f:id:ReK2Science:20200927001057p:plain — 1自由度系における振動

この時の運動方程式は，

$\displaystyle{ m \frac{d^2x}{dt^2} = -kx -c\frac{dx}{dt} }$

こうなります．この微分方程式は，定数係数線形斉次微分方程式と呼ばれます．この一般解は簡単に求めることができます．ですが，場合分けを行う必要があります．ここでは，不足減衰と呼ばれる場合を紹介します．一般解は以下のようになります．

$\displaystyle{ \zeta = \frac{c}{2\sqrt{mk}} }$

$\displaystyle{ p = w_n \sqrt{1 - \zeta^2} }$

とすると，積分定数を $\displaystyle{X}$ ， $\displaystyle{\alpha}$ として，

$\displaystyle{ x = Xe^{ - \zeta w_nt } cos(pt - \alpha) }$

となります．そして，この以下の図のようなグラフとなります．

f:id:ReK2Science:20200926235834p:plain — 様々な振動

このグラフは， $\displaystyle{\zeta}$ の値により，形が変わります．

このように，微分方程式を解き，振動の様子を検証することができます！

おわりに

いかがでしたか?

今回は，工学（電気回路・材料力学・機械力学）で応用されている微分方程式の具体例を紹介していきました．

微分方程式は，たくさんの分野で応用されていますね．

しかし，まだまだこんなものではありません．今回紹介しきれなかった応用例はたくさんあります．

少しは，

「微分方程式のイメージがつかめた気がする！！」

「微分方程式ってこういう場面で使うんだ！！」

となりましたか？

そして，ようやく次回から，詳しい微分方程式の解法を紹介していきます！

▽前回の記事▽

www.rek2u.com

本日も、りけいのりがお届けしました。

○2022年のお知らせ

りけいのりの中の人が、YouTubeチャンネルを開設しました！

りけい大学院生の日常や考えていることを共有していきます！！

記事の内容も動画にて再度取り上げる予定ですので、ぜひお立ち寄りください！！！

www.youtube.com

参考文献

１）矢野健太郎　石原繁　（1981），基礎解析学（改訂版）第38版，裳華房

２）高遠節夫　ほか　（2014），新応用数学　4版，大日本図書

３）馬場敬之　，スバラシク実力がつくと評判の力学キャンパス・ゼミ　改訂２，マセマ

４）西巻正郎　森武昭　荒井俊彦　（1990），電気回路の基礎（第三版），森北出版株式会社

５）西巻正郎　下川博文　奥村万規子　（1995），続　電気回路の基礎（第三版），森北出版株式会社

６）西村尚　（1988），ポイントを学ぶ材料力学（第36版），丸善出版

７）西村尚　（2004），機械力学（第12版），コロナ社

2020-12-11

【2020年】現代の地球環境問題を俯瞰する。土壌汚染の性質から重金属汚染まで。

環境学

本日も、りけいのりからお届けします。

我々を取り巻く環境汚染問題

近年、マイクロプラスチックによる海洋汚染問題や、化石燃料の利用に関する資源・エネルギー問題、気候変動や異常気象に伴う生物種の存続に関わる危機など、人類を取り巻く環境問題は著しいです。

我々人類は、産業革命以降、科学技術を積極的に活用して生活水準の向上を図ってきました。そんな科学技術が"両刃の剣"であることを人類が実感したのは、

鉱山廃水に由来する重金属の環境放出に伴う健康被害の顕在化
農薬の過剰使用に伴う生体濃縮と生物の死滅
化学物質のキラリティーと薬理活性の変化に伴う奇形児の誕生

などのセンセーショナルな事件です。科学技術による被害を受ける度に、人類は法改正や企業努力、環境浄化技術の開発を通して、問題に取り組んできました。

新しく何かを始める上では、予測可能な問題と予測不可能な問題が発生します。特に、予測可能な問題に対しては積極的な働きかけにより、無害化、もしくは問題の最小化をすることが望まれます。

本シリーズでは、我々を取り巻く環境汚染問題の現状を把握することを目的として、土壌環境、水環境、大気環境における環境問題の現状を俯瞰します。今回は、土壌環境編です。

f:id:ReK2Science:20201126173347p:plain

我々を取り巻く環境汚染問題
土壌環境の性質と汚染の移動
土壌汚染問題
おわりに
- 参考文献

土壌環境の性質と汚染の移動

まずは、土壌環境が汚染された場合における、被害の特徴について考えます。

f:id:ReK2Science:20201201100239p:plain — 物質の三態と拡散のアナロジー

ここでは、物質の三態と環境汚染物質の拡散のアナロジーを用いると、土壌汚染に対する理解が深まります。土壌汚染を構成するのは、固体である土壌になります。物質の三態の中で、固体はもっとも原子・分子同士の間隔が密であることが特徴です。原子や分子間の間隔が密であることに起因して、お互いの相互作用は大きくなります。

分子間の距離に依存して、クーロン相互作用や疎水性の相互作用が起こります。また、分子が密であることに起因して、物質の平均自由行程 (分子間の衝突なしに進める距離)は小さくなります。以上のことから、土壌環境に環境汚染物質が放出された場合、次のような特徴を示します。

土壌中の環境汚染物質は拡散が難しい。汚染の移動が水環境、大気環境と比較して小さい。

土壌中の環境汚染物質の分離は難しい。分子間に強い相互作用が働いており、分離にはエネルギーを要する。

土壌中の環境汚染物質は検出が難しい。土壌中では分子が密に存在しており、感覚器を通しての検出等が困難である。よって、汚染の発見が遅れる場合が多い。

端的には、以上が土壌汚染の性質となります。このことを踏まえて、2020年現在における土壌汚染の現状を俯瞰してみましょう。

土壌汚染問題

土壌汚染問題を把握する上で重要なポイントが2点あります。

土壌汚染対策法のカバーする土壌は地表から深さ10m

土壌汚染は自然に発生する場合、人間の活動に伴い発生する場合がある

参考: *1

特に、後者は重要な観点です。環境汚染をイメージすると、多くの方は人間の生産活動に伴って生じた環境被害をイメージすることが多いことかと思います。しかし、鉱脈等から流出する重金属等は自然由来の汚染であり、我々人類は予防をすることが出来ない問題も存在するのです。汚染とは、あくまでも人類を主体としたときの、主観的な事象に過ぎないことが分かります。

土壌汚染に関する近年の推移は次の通りです。

f:id:ReK2Science:20201201104528p:plain — 年度別の土壌汚染判明事例件数*2

土壌汚染関連法の施工に伴い、2018年における調査事例は2000年と比較して11倍程度となっています*2a。

土壌汚染において着目すべきは、次の物質です。

重金属：鉛、ヒ素、カドミウム (以下の図参照)
有機化合物：トリクロロエチレン、1,2-ジクロロエチレン等の有機塩素化合物
その他：フッ素

f:id:ReK2Science:20201201110224p:plain — 環境省, 平成28年度土壌汚染対策法の施行状況及び土壌汚染調査・対策事例等に関する調査結果

以上をまとめると、次のように結論付けられます。

未調査の土壌汚染は多数存在することが予想されることから、今後も環境のモニタリングが重要となる。
重金属においては鉛が主な汚染物質である。
有機化合物として、トリクロロエチレン等の有機塩素化合物による汚染除去も重要な課題となる。

国外においては、未だ土壌汚染は発生しています。処理の難しい土壌汚染に対する環境計測・浄化技術の開発、普及が求められます。

おわりに

現代における、主な土壌汚染問題は○○であることを学びました。一方で、前述の通り、土壌汚染の発見は難しいことから、今後も土壌汚染の新規件数は一定程度見込まれます。

また、環境を連続的に捉えることも重要です。環境を大雑把に土壌環境、水環境、大気環境と分類しましたが、あくまでもこれらは便宜上大別した環境区分です。土壌環境と水環境、大気環境の境目は極めて曖昧であり、異なる環境間で常に物質交換が起こっているといえるでしょう。つまり、土壌汚染は水質汚染、大気汚染につながるということです。

今後も注意深く、土壌汚染問題の動向をチェックすることが求められます。以上、りけいのりがお届けしました。

参考文献

*1:

大岩敏男, 大木久光, 高堂彰二, 保坂義男 (2014), 今日からモノ知りシリーズトコトンやさしい環境汚染の本, 28 土壌汚染.

*2:

令和２年版環境白書・循環型社会白書・生物多様性白書 (2020), 環境省, 第4節土壌環境の保全, a: 1. 土壌環境の現状.

www.env.go.jp

2020-12-10

【環境学】Introduction

環境学

本日も、りけいのりがお届けします。

今回は、新テーマ開設のお知らせです。テーマはズバリ、、

f:id:ReK2Science:20200921074220p:plain

導入
りけいのりは環境学の研究者
おわりに

導入

そうです。環境学についてです。環境学というと、非常に漠然としたイメージを持たれますが、まさしく漠然とした学問といえるでしょう。その理由は、対象が環境であることによります。

"Oxford Languages" の定義によると、環境とは、

人間または生物を取り巻く、まわりの状況。そのものと何らかの関係を持ち、影響を与えるものとして見た外界。

と、やっぱり漠然としているのです。なので、ざっくりと生物と非生物が織り成す世界、という認識で良いと思います。"まわりの状況"、"何らかの関係を持ち"と、環境を考える上で大切な要素が沢山出てきます。

すなわち、我々ホモサピエンスは、我々を取り巻く周りの世界に影響を及ぼし、反対に与えられていたりするのです。以下に例を見てみましょう。

地球温暖化問題

産業革命に伴い、地中に埋まっていた炭素源である化石燃料を燃やすことで、人は大きな動力源を得た。
ヒトは、化石燃料を利用したことで、二酸化炭素やメタンガスを大気中に放出し続けている。
二酸化炭素やメタンガスなどの温室効果ガスは、太陽光線に含まれる赤外高専のエネルギーを吸収する。
吸収されたエネルギーが、温室効果ガスの振動エネルギーに変換され、気温の上昇が発生する。
気温の上昇を受けて、気候変動が発生し、地球環境に大きな影響を及ぼす。
人類の生活にも影響が生じる。

このように、ある事象が発生すると、物理学、化学、生物学の垣根を超えた影響が地球全体に派生し、結果としてヒトが被害を被る構図が完成するのです。環境学では、このような外界と対象物の相互作用関係が大切になります。

前述の通り、環境の理解、すなわち環境学の修学には、サイエンスのありとあらゆる知識が必要となります。例えば、環境に関する理学的な探求だけでも、

分子生物学
熱力学
物理化学

と、様々な分野の知識が必要となる。環境学は、学際分野といえるでしょう。

f:id:ReK2Science:20200921153036p:plain

現代社会において、環境を理解することは、必須であると言えます。

子供
学生
ビジネスパーソン、などなど...

全人類が学ぶべき教訓が含まれています。それは、この地球環境は1つであり、ある1点での事象が地球全体に派生する、ということです。人間は、地球の大きさと比較すると非常に小さい生き物なので、地球規模での環境の変動を感知しずらいです。しかし、我々人間の与える環境への影響は大きく、単一の生物種: ホモサピエンスが大地を抉り、湖を造り、河川を引くようになりました。

もはや、地球に対して小さな人間は、大きな影響力を持っているのです。だからこそ、人間一人ひとりが、環境に対する正しい知識と理解を得て、科学的な根拠を基に行動を見直す必要があるのです。

2020-12-09

【色素から薬まで】アルカロイド大全②【神経伝達物質を中心に】

化学

本日も、りけいのりがお届けします。

今回は、前回に引き続き、多種多様な機能・構造を有するアルカロイドに迫ります。

www.rek2u.com

復習として、アルカロイドの特徴を箇条書きにしてみました。

アルカロイドはタンパク質や核酸などを除いた窒素を含む化合物の総称
アルカロイドは窒素にゆらいしてわずかに塩基性を示すことから酸に可溶
アルカロイドは、特定の構造を指し示す定義ではない

有機化合物の命名としては、汎用性の高い定義であることが分かります。

アルカロイドは、構造中に窒素を含みます。この構造的特徴は、生理活性が大きいことと深く関係しています。我々のカラダを構成する分子は、タンパク質、炭水化物、核酸などが挙げられますが、タンパク質と核酸は漏れなく窒素を含有しています。つまり、生体分子と類似の構造をアルカロイドが有することで、代謝に様々な影響を与えるのです。

有機化合物の骨格は炭素です。しかし、それだけでは無味乾燥な有機物しか合成されません。アルカロイド中に存在する窒素や、大気中に豊富に存在する酸素が、炭化水素に参加することで、初めて豊な性質を発現するのです。窒素はいわば、炭素のお化粧といえるでしょう。

我々の脳内には、窒素でお化粧された炭素が溢れています。これらの化合物は神経伝達物質と呼ばれ、我々の感情や、体調をコントロールしています。今回は、神経伝達物質としてのアルカロイドをまとめました*1 *2。

f:id:ReK2Science:20201126172039p:plain

神経伝達物質としてのアルカロイド
おわりに
- 参考文献

神経伝達物質としてのアルカロイド

セロトニン(Serotonin): 神経伝達物質, 危険行動抑制など*1a

f:id:ReK2Science:20201130123139p:plain

Structure and Property were refered from *3.

ノルアドレナリン(Norepinephrine): 神経伝達物質, 緊張・興奮状態の伝達*1b

f:id:ReK2Science:20201130123230p:plain

Structure and Property were refered from *4.

アドレナリン(Adrenaline): 神経伝達物質, 交感神経作用時の興奮などに関与*1c

f:id:ReK2Science:20201130123300p:plain

Structure and Property were refered from *5.

アセチルコリン(Acetylcholine): 神経伝達物質、副交感神経作用時のリラックス状態などに関与*1b

f:id:ReK2Science:20201130123335p:plain

Structure and Property were refered from *6.

GABA (γ-アミノ酪酸): 抑制性シナプス伝達、神経細胞の活動性を下げる*2

f:id:ReK2Science:20201130123403p:plain

Structure and Property were refered from *7.

おわりに

いかがでしたか? アルカロイドは、現在この記事を読んでいるあなたの頭の中でも活発に動作しており、"思考という行為そのもの"に貢献している物質です。そんなアルカロイドに注目すると、今までと違った世界が見えてくるかもしれませんね。

タンパク質を構成するアミノ酸に関しては、以下の記事で詳しく紹介しています。窒素がいずれの分子にも含まれていることが実感できます。

www.rek2u.com

核酸の中でも重要な塩基については、以下の記事について詳しく解説しました。

www.rek2u.com

以上、りけいのりがお届けしました。

参考文献

*1:

中村克樹, 徹底図解脳の仕組み, 株式会社新星出版社, a: 感情と情動のしくみ③p20, b: 体内環境を整える脳①p82-83, c: 感情と情動のしくみ②p8.

*2:

脳科学辞典、GABA、Accessed: 2020/11/30.

bsd.neuroinf.jp

*3:National Center for Biotechnology Information (2020). PubChem Compound Summary for CID 5202, Serotonin. Retrieved November 26, 2020 from https://pubchem.ncbi.nlm.nih.gov/compound/Serotonin

*4:National Center for Biotechnology Information (2020). PubChem Compound Summary for CID 439260, Norepinephrine. Retrieved November 26, 2020 from https://pubchem.ncbi.nlm.nih.gov/compound/Norepinephrine

*5:National Center for Biotechnology Information (2020). PubChem Compound Summary for CID 5816, Epinephrine. Retrieved November 26, 2020 from https://pubchem.ncbi.nlm.nih.gov/compound/Epinephrine

*6:National Center for Biotechnology Information (2020). PubChem Compound Summary for CID 187, Acetylcholine. Retrieved November 26, 2020 from https://pubchem.ncbi.nlm.nih.gov/compound/Acetylcholine

*7:National Center for Biotechnology Information (2020). PubChem Compound Summary for CID 119, gamma-Aminobutyric acid. Retrieved November 26, 2020 from https://pubchem.ncbi.nlm.nih.gov/compound/gamma-Aminobutyric-acid